por SOFIA ROMAN HIDALGO hace 6 meses
87
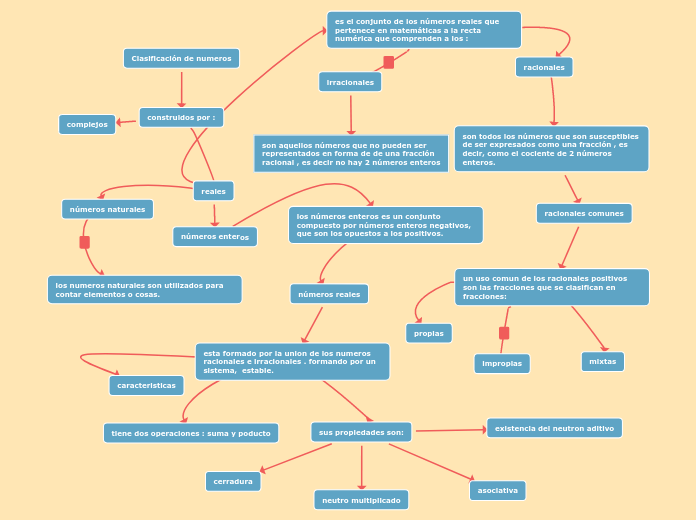
CADA NÚMERO, EN SU CONJUNTO
El texto abarca varios conceptos matemáticos fundamentales. Primero, describe los intervalos y semirrectas, destacando intervalos abiertos y cerrados, y cómo se representan matemáticamente.