作者:YESENIA MARIA AGUIRRE NUÑEZ 2 年以前
187
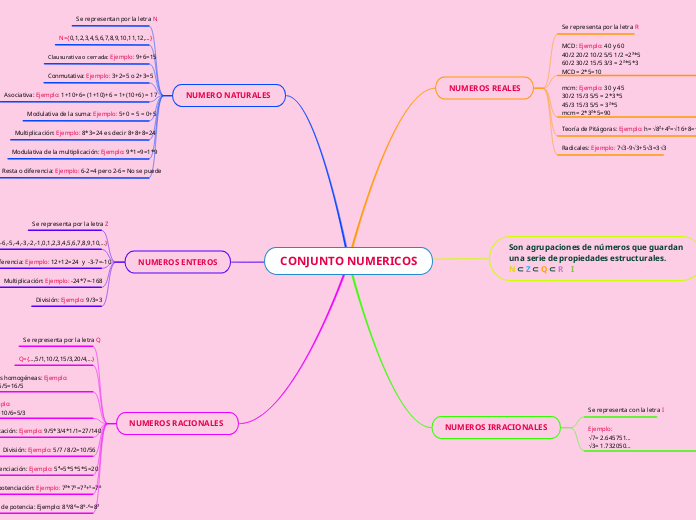
CONJUNTO NUMERICOS
Los conjuntos numéricos abarcan diferentes categorías, cada una con propiedades y operaciones específicas. Los números naturales incluyen el cero y todos los números positivos, y se caracterizan por propiedades como la conmutativa y la asociativa en la suma y la multiplicación.