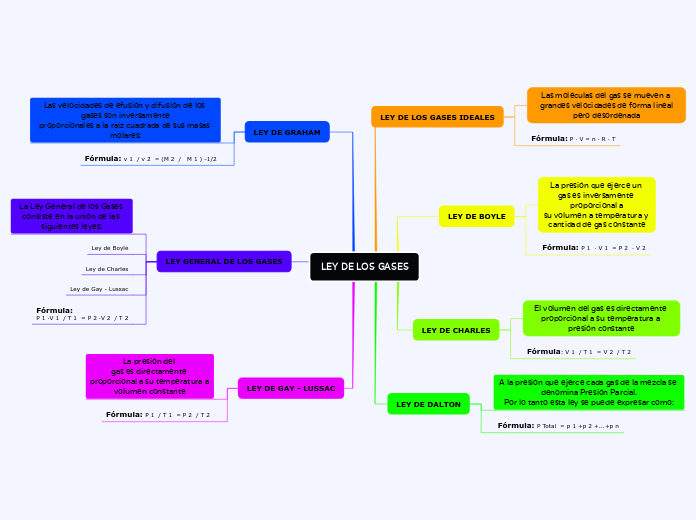
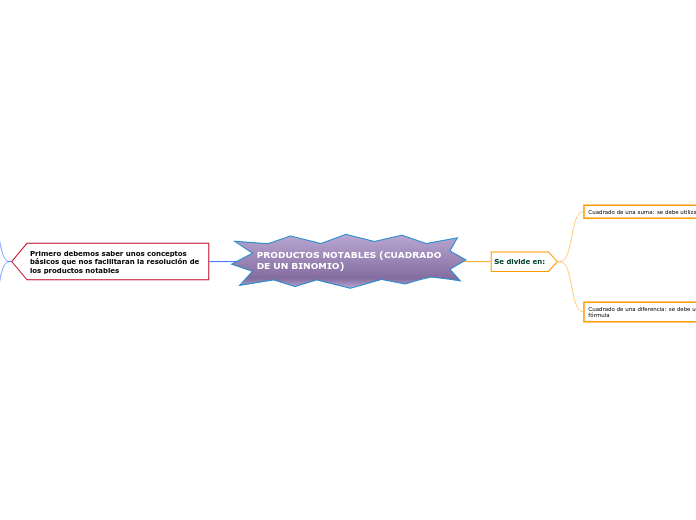
av Lucio Nilson Juarez Graos för 4 årar sedan
977
superficies en el espacio
Se describen varias superficies cuádricas, cada una con sus características y fórmulas asociadas. El cono elíptico es una figura que se genera al mover una recta a través de un punto fijo, apoyándose en dos elipses iguales y paralelas.