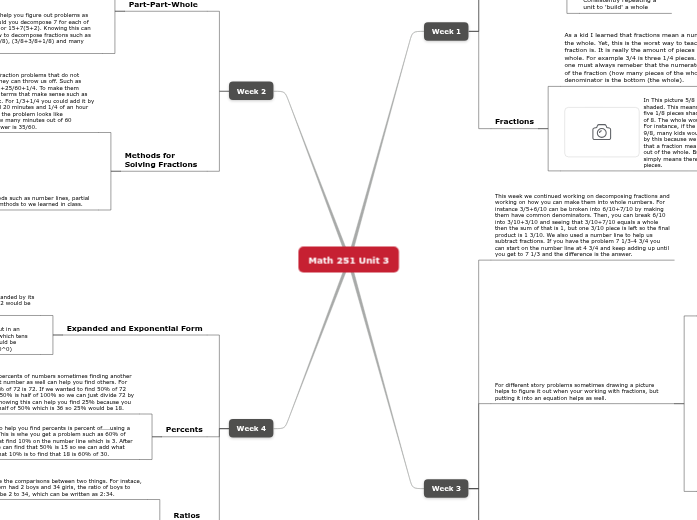
Math 251 Unit 3
Week 4
Ratios
Proportion and ratio tables help find things such as the amount of items you can get at a certain price.
For example: One fruit basket costs $15, how many fruit baskets can you buy with $135. If you put this in a table you could find that 1 would be $15, 2 would be $30, 4 would be $60, 8 would then be $120 and then we know that you could get 9 for $135.
Ratios make the comparisons between two things. For instace, if a classroom had 2 boys and 34 girls, the ratio of boys to girls would be 2 to 34, which can be written as 2:34.
Percents
Another way to help you find percents is percent of....using a number line. This is whe you get a problem such as 60% of 30. We can first find 10% on the number line which is 3. After finding this we can find that 50% is 15 so we can add what 50% is and what 10% is to find that 18 is 60% of 30.
When finding percents of numbers sometimes finding another percent of that number as well can help you find others. For example, 100% of 72 is 72. If we wanted to find 50% of 72 we know that 50% is half of 100% so we can just divide 72 by 2 to get 36. Knowing this can help you find 25% because you can just take half of 50% which is 36 so 25% would be 18.
Expanded and Exponential Form
Exponential form is when you write the number out in an addition statement with exponents, representing which tens place the number goes in. For example, 1,342 would be written as (1*10^3)+(3*10^2)+(4*10^1)+(2*10^0)
Expanded form is when you show the number expanded by its digits in an addition statement. For example, 1,342 would be written as 1,000+300+40+2.
Week 2
Methods for Solving Fractions
You can also use other methods such as number lines, partial sums, traditional, and other mthods to we learned in class.
This picture shows an example of how someone could use a number line to add or subtract fractions.
Somtimes when you look at fraction problems that do not have common denominator they can throw us off. Such as problems like 1/3+1/4 or 1/3+25/60+1/4. To make them easier you can put them into terms that make sense such as minutes in an hour on a clock. For 1/3+1/4 you could add it by knowing 1/3 of an hour equal 20 minutes and 1/4 of an hour equals 15 minutes. So really, the problem looks like 20+15=35, but since it is how many minutes out of 60 minutes the final fraction answer is 35/60.
Fraction Sense: Part-Part-Whole
Decomposing numbers can help you figure out problems as well. For example: How would you decompose 7 for each of these problems? 9+7(6+1) or 15+7(5+2). Knowing this can also help you figure out how to decompose fractions such as 7/8 into (6/8+1/8), (5/8+2/8), (3/8+3/8+1/8) and many other ways
Decomposed fractions can also be the equivalent to other fractions and written in different ways, but they still are equivalent fractions and mean the same thing. For instance, 6/8+1/8=3/4+1/8 and 5/8+2/8=5/8+1/4. When you are adding two fractions and you want to simplify, sometimes using decomposing fractions can help you. For example, the problem 7/8+3/8. In this problem you could leave 7/8 as it is and decompose 3/8 into (1/8+2/8) so as to get to a whole and friendly number. This problem would be (7/8+1/8)=1. Thus, leaving the 2/8 left turning the problem into 1+2/8=1 2/8, which is your final answer.
This is decomposing or composing a number. The number 7 for instance could be decomposed into: (6+1), (4+3) or (5+2)
Here is a video on how to decompose fractions:
Week 3
When converting fractions into decimals and percents it can be tricky. For fractions such as 1/2 most people know that it equals .5 and 50%. When converting fractions such as 24/25 it can be tougher. An easy way to figure it out is to get to a power of ten. Decimals will always have a denominator that is to the power of 10 as well. Since 25 is greater than 10 we can go to the power of 100. The denominator 25 goes into one hundred 4 times. So since we know that we can multiple 24*4 to make it out of 100 which is 96. Now that you have this you can know your fraction is .96 and your percent is 96%.
When it comes to dividing fractions there are different ways such as inverting, partition, and repeated subtraction. Inverting is when you have a problem like 1/3 / 1/2. To solve this problem you can simply invert, or flip, the second fraction (the divisor) and always only the second fraction so that the problem turns into 1/3*2/1=2/3.
Sometimes when dividing fractions you'll come across fractions such as 9/167 / 3/167. For this problem you can invert the divisor to change the problm to 9/167*167/3. But since 167 can cancel each other out the problem can be reduced to 9/1*1/3=9/3 or 3. Sometimes you can solve problems without inverting such as 3/4 / 1/2 if you just divide across (denominator/denominator and numerator/numerator) the answer is 3/2. When dividing whole mixed number fractions it is usually easier to switch them to improper fractions.
For example: 2 1/4 / 3 3/5 can be made into the improper fractions 9/4 and 18/5. After that, you can find a common denominator which is 20 because both the denominators can go into it. But you have to multiply the numerators as well by the same number their denominator was multiplied by so the problem turns into 45/20 / 72/20. The denominators cancel each other out so the final answer is 45/72.
Partition is: (the dividend) split into (the divisor) groups. For example, 3/ 1/2 would be 3 split into 1/2 groups. But that doesn't seem to fit which is why you could use repeated subtraction: how many (divisor) are in (dividend), which would look like...how many 1/2 are in 3. This problem works better because it shows what the problem means, partition can too for the right problem.
For different story problems sometimes drawing a picture helps to figure it out when your working with fractions, but putting it into an equation helps as well.
When you multiply fractions you can simply just multiply across. For instance, 4/9*2/3=8/27. If you have a problem with whole numbers like 5 3/8*2, it helps to split the numbers up using the area model and then adding the sums of the numbers up at the end. Also, if you want to show the sum in an area model for 2/3*4/5 for instance, you would draw a box and divide it into 5 chunks vertically and color 4 of them. Then, you would divide those four shaded chunks into 3 rows horizontally and shade in 2 of them to represent 2/3. After your done shading you should have 8/15 of the rectangle shaded.
Here is a video to help show how to multiply and divide fractions. Although in the video they say you must always reduce the problem, this is not true. You do not have to reduce fractions.
For example: Miah had 4/6 of a pan of brownies left. Sarah came and bought 3/4 of what she had left. How many brownies did Sarah take out of the whole pan? So in this problem the equation would be she took 3/4 of 4/6, which is the same thing as 3/4*4/6 which equals 12/24 or 1/2. So Sarah took 1/2 the pan of brownies.
This week we continued working on decomposing fractions and working on how you can make them into whole numbers. For instance 3/5+6/10 can be broken into 6/10+7/10 by making them have common denominators. Then, you can break 6/10 into 3/10+3/10 and seeing that 3/10+7/10 equals a whole then the sum of that is 1, but one 3/10 piece is left so the final product is 1 3/10. We also used a number line to help us subtract fractions. If you have the problem 7 1/3-4 3/4 you can start on the number line at 4 3/4 and keep adding up until you get to 7 1/3 and the difference is the answer.
Week 1
Fractions
In This picture 5/8 of the cirlce is shaded. This means that there are five 1/8 pieces shaded, not 5 out of 8. The whole would be 8 pieces. For instance, if the fraction was 9/8, many kids would be confused by this because we are all taught that a fraction means a number out of the whole. But really that simply means there are nine 1/8 pieces.
When you are counting by fractions it is easiest to think of it kind of like counting by whole numbers. If you could up by two's you simply go: 2, 4, 6, 8. When you are counting up by say 2/3, you simply just count the numerator up by two's and the denominator stays the same like so: 2/3, 4/3, 6/3, 8/3. Notice how the numerator goes up by two's and the denomintor stays the same. You can use this when counting up by any fraction.
As a kid I learned that fractions mean a number out of the whole. Yet, this is the worst way to teach what a fraction is. It is really the amount of pieces out of the whole. For example 3/4 is three 1/4 pieces. In addition, one must always remeber that the numerator is the top of the fraction (how many pieces of the whole) and the denominator is the bottom (the whole).
Unit Iteration
Consistently repeating a unit to 'build' a whole
For example: Show me one whole using 1/5 pieces. You would start with the first one 1/5 pieces and add up until you came to five 1/5 pieces that would equal the whole. 5/5=the whole
Partitioning
'Splitting the whole into equivalent parts
Attached here is a link to a video that shows examples of partitioning. In the video, she breaks shapes into equal amounts of pieces. This is different than unit iteration because you are not repeating a unit to find the whole, you are simply divind the whole into equal parts from the beginning