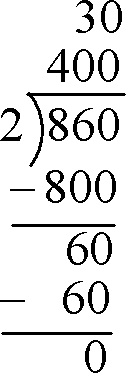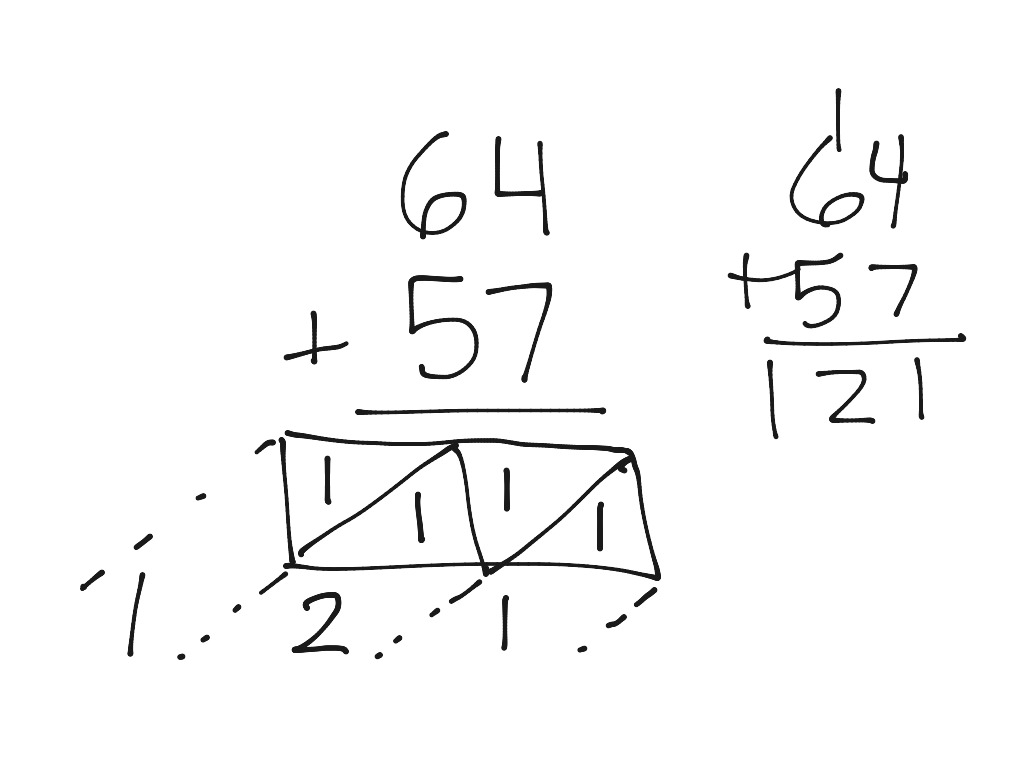MTE 280- Elementary Mathematics

Meer zoals dit

Real Numbers

door Rishie Rathi

MAT.105X A7

door David Kedrowski

Biology Study

door Anonymous User

Elementary Mathematics

door Jacklyn Martinez

MTE 280- Elementary Mathematics

Weeks 4-5

Addition Properties

Commutative Property

• Order does not make a difference in the answer
• Works only for addition/multiplication

Example:

2+9+3+1=15

9+1+1+3=15

Associative Property

• Grouping (parenthesis placement) does not make a difference in the answer
• Works only for addition/multiplication

Example:

(1+4)+6=11

1+(4+6)=11

Alternative Algorithms

• Write out the division problem
• Divide like the traditional algorithm, but with emphasis on place value

Example:

860/2

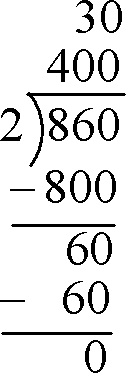
400+30=430

• Works if there is a non-zero remainder
• Repeatedly subtract from the number being divided
• Answer is the number of subtractions completed

Example:

18/6=3

1 subtraction: 18-6=12

2 subtractions: 12-6=6

3 subtractions: 6-6=0

• Draw out the base ten blocks representing the number being divided
• Starting with the largest place value, separate into groups of the what the number is being divided by
• Convert the remainder of that place value into the one below it
• Continue separating into groups and regrouping until there are units left that cannot make a group
• Write out the answer based on how many groups of each shape there are

Example:

726/6

*Brackets represent groupings

7 flats = [6 flats] + 1 flat

1 flat + 2 longs = 12 longs = [6 longs] + [6 longs]

6 units = [6 units]

6 flats + 2(6 longs) + 6 units =121

Expanded Form

• Write each number in its expanded form
• Subtract numbers from the same place value normally
• Add the expanded number together

Example:

525-422=

(500+20+5)-(400+20+2)=

(500-400)+(20-20)+(5-2)=

100+0+3=103

Friendly Numbers

• Goal: change some or all numbers to be multiples of ten
• Add to one number, subtract that from another number
• Subtract new numbers

Example:

57-21=

(57+1)-(21-1)=

58-20=38

• Draw the lattice structure
• Write each digit of each number along the top and right edges of the rectangle
• Multiply each edge, write the first digit in the top section and the second digit in the bottom section
• Add down the diagonals
• Answer is read from top left corner to bottom right corner

Example:

Area Model

• Similar to base ten blocks, but slightly more advanced
• Draw a rectangle
• On adjacent sides of the rectangle, write each number in its expanded form
• Extend lines through the rectangle wherever there are plus signs
• Multiply the numbers on the edges to find the area of each individual square
• Add the areas together to get the total area of the rectangle

Example:

Base Ten Blocks

• Draw a rectangle
• Along two adjacent edges of the rectangle, separate units, longs, and flats (or ones, tens, and hundreds)
• Continue the lines through the rectangle to separate the interior into flats, longs, and units
• Add up each section
• Add the section totals together

Example:

• Write numbers out in their expanded form
• Multiply each separate number
• Add the products

Example:

275+182=

(200)100=20000

(200)80=16000

(200)2=400

(70)100=7000

(70)80=5600

(70)2=140

(5)100=500

(5)80=400

(5)2=10

20000+16000+400+7000+5600+140+500+400+10=50,050

Compatible Numbers

• Same process as friendly numbers
• Subtract an amount from one number and add that amount to another
• Will not get all numbers into multiples of ten
• Goal: to turn some or all numbers into compatible numbers (numbers that are easy to use mentally)

Examples:

24+39+12=

(24+1)+(39+1)+(12-2)=

25+40+10=75

43+62+21=

(43+2)+(62-2)+21=

45+60+21=126

Friendly Numbers/Trade-Off

• Take away some from one number and give that amount to the other
• Goal of getting numbers to multiples of ten

Examples:

37+63=

(37+3)+(37-3)=

40+60=100

28+54+36+22=

(28+2)+(54-4)+(36+4)+(22-2)=

30+50+40+20=140

Left-to-Right

• Instead of adding starting at the ones place and working left, you start from the left and work right.

Example:

348

+ 891

---------

1100

130

+9

-----------

1239

Lattice

• Write numbers vertically
• Draw box underneath each place value
• Draw diagonal line through each box, extending from top right through bottom left corner
• Starting with the ones column, add numbers
• Write the sum's tens digit in the top section of the box and the ones digit in the bottom section
• Move onto the next column and add the same way
• Add down the diagonals, placing sum just outside the box
• Answer is read left to right

Example:

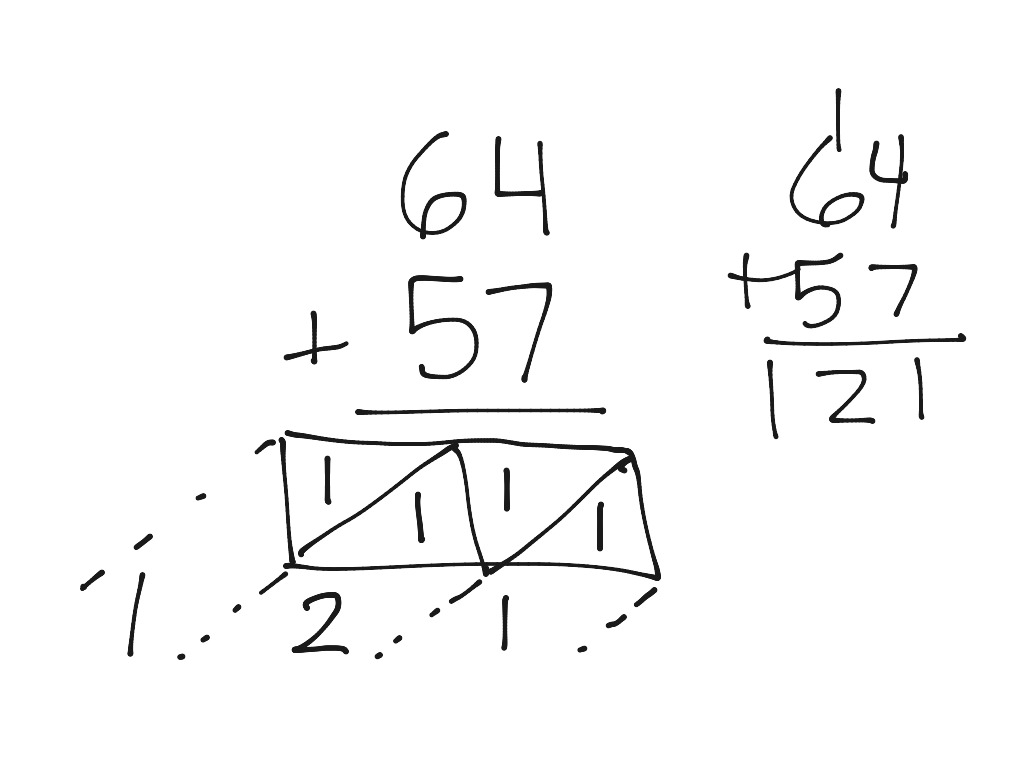
Expanded

• Use for adding large numbers with in hundreds or more
• Write out each number in its expanded form
• Add the expanded numbers

Example:

4615+3548

4000+600+10+5

+3000+500+40+8

________________

7000+1100+50+13=8163

Scratch

• Used for adding many numbers
• Write numbers vertically
• Start in ones column and add going down
• Scratch a number off once you get to 10 (or whatever the base is) and write the remainder next to it
• Continue adding going down and place the last remainder of the ones column under the addition bar
• Count up the number of scratches and write that number on top of the tens column
• Add up the tens column using the same process of scratches and remainders

Example:

2

31

8

27 6

2 51

62

+ 23 2

----------

202

Weeks 1-3

Base Conversions

Converting from Base Ten

Diagram Method (Show)

• Skip count to draw the given number using units, flats, and longs
• Count up the number of each: units, longs, and flats
• Write the number of each shape in their respective place values

Example: Convert 31 to base eight

• Skip count: 8, 16, 24 (draw 3 longs)
• Draw one unit for each remaining number (7 units)
• Write the answer as 37_eight

Algorithm Method (Solve)

• Use downwards division, dividing the base number into the given number

Example: Convert 31 to base eight

• 8 goes into 31: 3 times with 7 leftover
• 31=37_eight

Example: Convert 47 to base five

• 5 goes into 47: 9 times with 2 leftover
• 5 goes into 9: 1 time with 4 leftover
• 47=142_five

Converting to Base Ten

Diagram Method (Show)

• Draw out the given number using units, longs, and flats
• Write down the value of each shape
• Units=1, longs=x, Flats=(x)²
• Where x=number of base
• Add up the value of each shape

Example: Convert 23_five to base_ten

• 2 longs and 3 units
• Each long=5, each unit=1
• 2(5)+3(1)=13

Algorithm Method (Solve)

• Multiply number of flats by x²
• Multiply number of longs by x¹
• Multiply number of units by x⁰
• Sum the numbers

Example: Convert 23_five to base_ten

2(5¹)+3(5⁰)=13

Example: Convert 4,120,367_nine to base_ten

4(9⁶)+1(9⁵)+2(9⁴)+0(9³)+3(9²)+6(9¹)+7(9⁰)=2,198,239

Base Systems

Using Manipulatives and Models

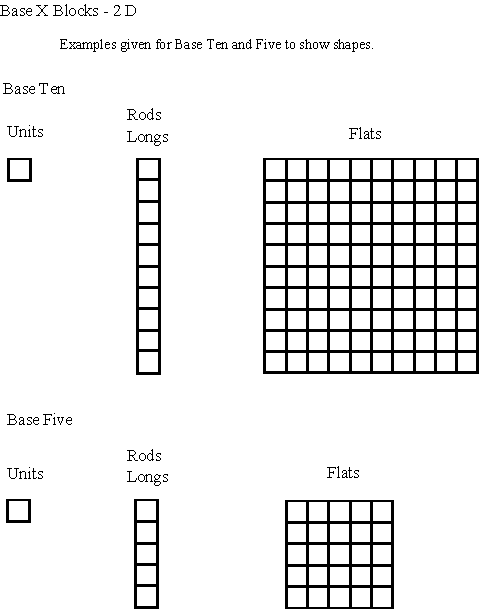
Place Values

Base Ten

• Ones, tens, hundreds
• Ones=10⁰
• Tens=10¹
• Hundreds=10²

Other Bases

• Units, long, flats
• Units=x⁰
• Longs=x¹
• Flats=x²
• x=base number

Other Bases

• Base is specified as subscript
• Counting in base_four: 1, 2, 3, 10
• Counting in base_thirteen: 1, 2, 3, 4, 5, 6, 7, 8, 9, T, E, W, 10

Base Ten

• Standard system of counting
• Created because humans have 10 fingers
• Assume base ten if no base is specified
• Counting in Base_ten: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Types of Logical Reasoning

Inductive Reasoning

Figuring something out based on a pattern

Deductive Reasoning

Figuring something out based on or using prior knowledge

Standards of Mathematics Practice

Problem Solving Strategies

• Look for the pattern
• Do an easier problem
• Modify the problem (get rid of the hard part)
• Draw a diagram
• Guess and check
• Write an equation

Common Core Standards

• Make sense of the problem
• Use abstract/quantitative reasoning
• Use logical arguments
• Use tools
• Understand structure
• Look for patterns of reasoning
• Model
• Use precision

4 Step Problem Solving Process

1. Understand the problem
2. Develop a plan to solve the problem
3. Carry out the plan
4. Look back- does the answer make sense?

Weeks 11-15

Percents

• Find 10%
• Multiply to get desired percentage
• Add 5% if needed
• Subtract from 100 first for discount problems

Example:

40% of 70

10% = 7

x4 x4

40% = 28

Decimals

Show:

• Draw out box, divide into ten
• Draw first number
• Divide box into ten the opposite way
• Draw second number
• Count how many boxes are shaded twice

Solve:

• Estimate answer by multiplying the whole numbers
• Write out multiplication problem without the decimals
• Multiply like normal
• Compare answer to estimate and add decimal where the answer is closest to the estimate

Show:

• Flat = unit
• Longc= tenth
• Unit = hundredth
• Draw out like fractions
• Addition: draw out box divided into ten, fill in decimals
• Subtraction: draw out box divided into ten, fill in first decimal, take away (cross out) second decimal

Solve:

• Line up the whole numbers and add normally

Multiplication Table

Order to teach multiplication table:

• Ones, twos
• Tens, fives
• Threes, Nines
• Doubles

Order of Operations

• GEMDAS
• Make groups
• Use EMDAS to simplify groups

Divisibility Rules

A number is divisible by x if...

2: Ones place is even

3: Sum of all digits is divisible by 3

4: Last two digits is divisible by 4

5: Ones place is 5 or 0

6: Divisible by 2 and 3

8: Last 3 digits is divisible by 8

9: Sum of all digits is divisible by 9

10: Ones place is 0

Division Algorithms

Repeated Subtraction

• Students don't need to know many multiplication facts
• Takes longer

Example:

52/3

3|52

-30| 10

22

-15| 5

7

-6|

1

=17 1/3

Upwards Division

• Write division problem as a fraction
• Divide denominator into each digit left-to-right

Example:

474=59 2/8

8

47/8

8*5=40

47-40=7

74/8

8*9=72

74-72=2

Weeks 6-10

Fractions

What is a fraction?

• Parts of a whole
• Numerator (top number): how many pieces you have
• Denominator (bottom number): what size the pieces are

Comparing Fractions

• Determine if fraction is >, <, or = to another fraction
• > greater than
• < less than
• = equal than
• Methods:
• Anchor fractions: simple fractions to compare each fraction to (1/2, 1, etc.)
• Whole numbers: whichever number has the larger whole number is greater
• Same denominator: whichever fraction has the same numerator is greater
• Same numerator: whichever number has the smaller denominator is greater (because they have the same number of pieces, but a smaller denominator means bigger pieces)

Show:

• When # of groups = fraction:
• Draw a full group and fill in with the number inside the group
• Draw a box around how much of the group you want
• Example: 1/2(4)
• Draw a group with 4 dots inside
• Draw a box around 1/2 of the group
• Answer = 2 because 2 dots are boxed
• When number inside the group = fraction:
• Draw number of groups
• Inside each group, draw a box to represent the fraction
• Add the fractions together
• When both numbers are fractions:
• Draw a box
• Divide box vertically by first denominator and divide box horizontally by second denominator
• Shade in vertically based on first numerator and shade in horizontally by second numerator
• Answer: numerator = number of boxes that are double shaded, denominator = numbers of boxes total

Solve:

• Multiply numerator by numerator and multiply denominator by denominator
• Example: (2/3)(1/4) = (2/12)

Addition/Subtraction

Show:

• Draw two same-sized boxes
• Divide first box vertically based on the first fraction's denominator
• Divide second box horizontally based on the second fraction's denominator
• Shade in each box based on its respective numerator
• Copy the dividing lines from one box onto the other and vice versa
• Draw a third box with the vertical and horizontal dividing lines
• Shade in the third box by counting the number of small sections in the first and second boxes

Solve:

• Two fractions must have common denominators to be added or subtracted
• If denominators are the same, add or subtract the numerators and keep the denominator
• If denominators are different, find a common denominator:
• Factor each denominator using one common factor
• Whatever is missing from each denominator, multiply by it as a fraction equal to one (x/x=1)
• Denominators are the same, add or subtract numerators and keep the denominator

Factoring

Least Common Multiple

• The smallest multiple that two numbers have in common
• List out all factors of each number
• Add the biggest exponent on each number

Example: 20 and 18

20 = 2*3²

18 = 2²*5

LCM = 2²*3²*5

Greatest Common Factor

• The largest factor that is common for two different numbers
• Using each number's prime factorization, the GCF is all of the factors the two have in common, with the lowest exponent present for each

Example: 20 and 18

20 = 2*3²

18 = 2²*5

GCF = 2

Prime Factorization

• Factors: numbers multiplied together to get an answer
• Prime: a number with exactly 2 factors
• Composite: a number with more than 2 factors
• Prime factorization: factoring a number using only prime numbers

Downwards Division

• Use downwards division, but the number on the left must be prime

Example:

3 L24

2 L8

2 L4

2

24 = 2³*3

Factor Trees

• Draw any two factors coming down from number
• Keep drawing two factors for each next number until left with only prime numbers

24

^

12*2

^

6*2

^

3*2

24 = 2*2*2*3 = 2³*3

Integers

Absolute Value

• Value of a number without its sign

Example: Abs. value of -12 is 12. Abs. value of -53 is 53.

Division

Solve:

• Divide numbers like normal
• If signs are the same, answer is positive
• If signs are different, answer is negative

Multiplication

• First number is # of groups, second is what's in each group
• 2(3) is 2 groups of 3
• -2(3) is like 0-2(3)

Show:

• Draw circles to represent groups, fill in groups with + or - to represent what's in each group
• For problems where the first number is negative:
• Create zero banks first
• Circle and arrow what is being taken away

Solve:

• Multiply numbers like normal
• If the signs are the same, answer is positive
• If the signs are different, answer is negative
• Example:
• -2(3)=-6
• -2(-3)=6
• 2(3)=6
• 2(-3)=-6

Subtraction

• Say "take away" instead of "minus" or "subtract"
• Difference between take away and negative:
• Take away is an action
• Negative is a description

Show:

• Draw out + and - for what you have
• Circle what you are taking away and draw arrow
• Answer is whatever is left after taking away

Solve:

• Use "Keep, change, change"
• Keep the first number's sign, change the subtraction to addition, change the second number's sign

Addition

Show:

• Draw out + and - for what you have (the first number)
• Draw out + and - for what is added
• Circle zero pairs (pairs of one + and one -, which add up to zero)
• Answer is what is left without zero pairs

Solve:

• Draw two + or - under whichever number is larger (absolute value)
• Draw one + or - under whichever number is smaller (absolute value)
• Circle one sign under one number and one sign under the other number
• If the signs circled are the same, add
• If the signs circled are different, subtract
• The sign left out of the circle is the sign the answer will have