Gráficas de control

More like this

Espacio Marino Venezolano.

by Isaac Mendoza

la guerra del pacifico

by AYLIN ALIANNA LEON BERNAL

Posición Global del Istmo de Panamá

by iris quintero

7 HERRAMIENTAS DE LA CALIDAD

by LUIS ALFONSO

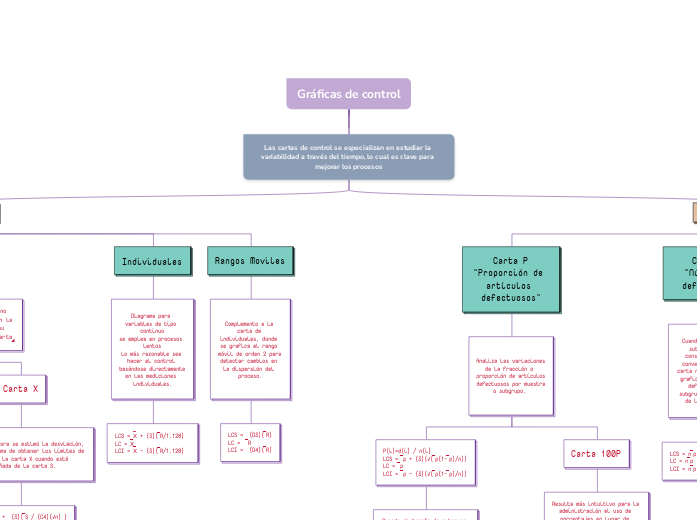
Gráficas de control

Las cartas de control se especializan en estudiar la variabilidad a través del tiempo, lo cual es clave para mejorar los procesos

Por Atributos

Carta U "Número de defectos por unidad"

Cuando en el tipo de variables con distribución Poisson, el tamaño del subgrupo no es constante, se analiza la variación del número promedio de defectos por artículo o unidad, en lugar del total de defectos en el subgrupo.

LCS = ̅u + (3)(√( ̅u/n)) LC = ̅u LCI = ̅u - (3)(√ ( ̅u/n))

Cuando el tamaño de subgrupo n no se mantiene constante a lo largo de las muestras, se tienen dos alternativas.

Carta con límites variables

Usar el tamaño promedio del subgrupo ̅n en lugar de n.

Carta C "Número de defectos"

Analizar la variabilidad del número de defectos por subgrupo, cuando el tamaño de éste se mantiene constante.

LCS = ̅c + (3)(√ ̅c) LC = ̅c LCI = ̅c - (3)(√ ̅c)

Carta NP "Número de defectuosos"

Cuando el tamaño de subgrupo p es constante, es más conveniente usar la carta np, en la que se grafica el número de defectuosos por subgrupo di, en lugar de la proporción.

LCS = n ̅p + (3)(√(n ̅p(1- ̅p))) LC = n ̅p LCI = n ̅p - (3)(√(n ̅p(1- ̅p)))

Carta P "Proporción de artículos defectuosos"

Analiza las variaciones de la fracción o proporción de artículos defectuosos por muestra o subgrupo.

Carta 100P

Resulta más intuitivo para la administración el uso de porcentajes en lugar de proporciones, se multiplica por 100 toda la escala de la carta p

P(i)=d(i) ⁄ n(i) LCS = ̅p + (3)(√( ̅p(1- ̅p)/n)) LC = ̅p LCI = ̅p - (3)(√( ̅p(1- ̅p)/n))

Cuando el tamaño de subgrupo n no se mantiene constante a lo largo de las muestras, se tienen dos alternativas.

Usar el tamaño promedio del subgrupo n en lugar de n. Esta alternativa se recomienda cuando la variación entre los tamaños de subgrupo no es demasiada (menor a 20% es aceptable).

Carta P con límites variables

Los límites de control van cambiando su amplitud dependiendo del tamaño de cada subgrupo ni.

LCS = ̅p + (3)(√( ̅p(1- ̅p)/ni)) LC = ̅p LCI = ̅p - (3)(√( ̅p(1- ̅p)/ni))

De variables

Rangos Moviles

Complemento a la carta de individuales, donde se grafica el rango móvil de orden 2 para detectar cambios en la dispersión del proceso.

Individuales

Diagrama para variables de tipo continuo se emplea en procesos lentos lo más razonable sea hacer el control basándose directamente en las mediciones individuales.

LCS = X̅ + (3)( ̅R/1.128) LC = X̅ LCI = X̅ - (3)( ̅R/1.128)

Carta X-S

Si n > 10 la carta de rangos ya no eficiente para detectar cambios en la variabilidad del proceso y en su lugar se recomienda utilizar la carta S

Carta X

La forma que ahora se estimó la desviación, modifica la forma de obtener los límites de control de la carta X cuando está acompañada de la carta S.

LCS = X̅ + (3)( ̅S / (C4)(√n) ) LC = X̅ LCI = X̅ - (3)( ̅S / (C4)(√n) )

Carta S

Por lo general en un estudio inicial no se conoce la desviación, puede estimarse.

LCS = X̅ + (3)( ̅S/C4)(√1-C4^2) LC = ̅S LCI = X̅ - (3)( ̅S/C4)(√1-C4^2)

Carta X̅-R

Se usa en procesos masivos y con variables de salida de tipo continuo.

Carta X̅

Analiza la variación entre las medias de los subgrupos, para detectar cambios en la media del proceso.

LCS = X̅ + (A2)( ̅R) LC = X̅ LCI = X̅ - (A2)( ̅R)

Carta R

Analiza la variación entre los rangos de los subgrupos, lo cual permite detectar cambios en la amplitud o magnitud de la variación del proceso.

LCS = (D3)( ̅R) LC = ̅R LCI = (D4)( ̅R)