Math in Motion
The goal of this mind map is to outline online resources and general information that can be useful for teaching measurement and motion in geometry to first thru sixth grade.
Congruence Mapping
This subject could be covered with advanced elementary students or added if teaching an extended school year. If desired to add to teaching curriculum it would fit nicely during the tessellation unit.
Composition of Mappings
Tessellations
Congruence
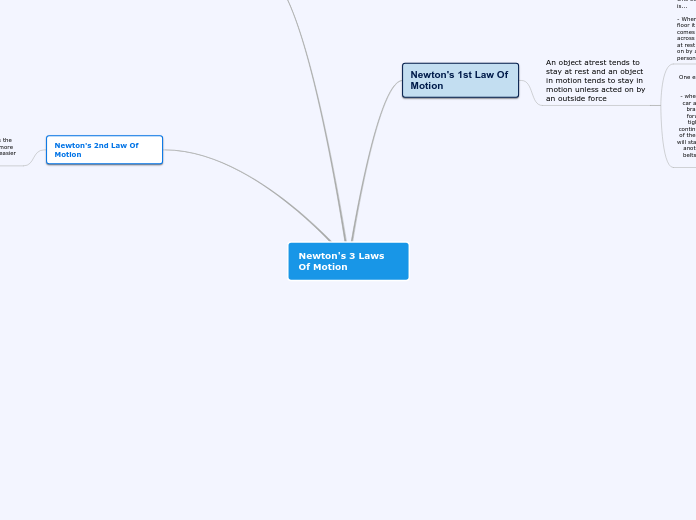
Congruent Figures: Two geometric figures are congruent if and only if there exists a translation, reflection, rotation or glide reflection of one figure onto the other.
Rotations
Rotations can be confusing for the students, use foam shapes or virtual manipulative for classroom demonstrations
Reflections
Translations
Translation is a special kind of mapping using a sliding motion.
Congruence
and
Constructions
Congruence is if one can be placed on the other so that they both coincide.
Circumscring Circles About Triangles
Perpendiculars and Parallel Lines
Bisectors
Bisecting Segments and Angles
Perpendicular Bisector
Side-Side-Side (SSS) Congruence Propery
If three sides of one triangle are congruent to three sides of another triangle, the two triangles are congruent.
Triangle Inequality
The sum of the lengths of any two sides of a triangle is greater than the length of the thrid side.
Side-Angle-Side (SAS) Congruence Propery
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the two triangles are congruent.
Angle-Side Angle (ASA) Congruence Property
If two angles and the included side of one triangles are congruent to two angles and the included side of another triangle, the triangles are congruent.
Constructing Segments and Angles
Mapping
Congruent polygons are two polygons that have corresponding sides and corresponding angles that are congruent.
Volume and Surface Area
Volume and Surface Area of Space Figures
Irregular Shapes
The volume of some items is most easily found by submerging in water. This is achieved by measuring the amount of water that is displaced.
Spheres
Surface area of sphere = 4 x pi x r squared
Volume of sphere = 4/3 x pi x 4 cubed
Cones
Pyramids
Cylinders
Surface area of cylinder = (2 x pi x h) + (2 x pi x r squared)
Volume of cylinder = b x h
Prisms
This picture can be enlarged for a classroom poster.
Surface Area
Standard Units of Volume
There is a corresponding unit of volume, cubic. Shapes are three dimensional.
Metric Units
English Units
Nonstandard Units of Volume
Area
and
Perimeter
Area is the number of units it will take to cover a surface.
Perimeter is the length of the boundary of a surface.
Areas
Circles
Circumference is the distance around the circle.
To find the circumference take the diameter (the distance across a circle through the center point) x pi (3.1416)
Area of circle = pi (3.1416) x radius (r) squared
Polygons
Trapezoids
Area of trapezoid = 1/2 x [upper base (u) + lower base (b)] x height (h)
Triangles
Area of triangle = 1/2 x base (b) x height (h)
Parallelograms
Area of rectange = length (l) x width (w)
Area of parallelogram = base (b) x height (h)
Perimeter
Standard Units of Area
Nonstandard Units of Area
Systems of Measurement
International System of Units
The metric system is established as the International system of units. It also includes second for time, ampere for electric current, candela for light intensity and mole for molecular weigh of a substance.
Metric units
Metric Units for Mass
Kilogram kg 1000 grams
Hectogram hg 100 grams
Dekagram dag 10 grams
Gram g 1 gram
Decigram dg 1/10 gram
Centigram cg 1/100 gram
Milligram mg 1/1000 gram
History of the Celsius temperature scale:
Anders Celsius early became engaged in the general problem of weights and measures, including temperature measurements. Already as a student he assisted the astronomy professor Erik Burman in meteorology observations. At that time there existed a large variety of thermometers with different scales. Perhaps he already at this stage realized the necessity of a common international scale.
A temperature scale must be based on one or two standard temperatures, called fixed points. For those it was natural to choose temperatures within the temperature domain of practical interest, i.e. from about plus forty to minus twenty in modern Celsius degrees. Thermometers were simply used in meteorology, in horticulture, and sometimes for indoor use. As fixed points one could use the human body temperature or temperatures of local origin such as the observatory cellar in Paris or the highest temperature in sunshine in London. Of course also the freezing and boiling points of water were used, but it was not self-evident that they really were universal and e.g. independent of the geographic latitude.
Anders Celsius should be recognized as the first to perform and publish careful experiments aiming at the definition of an international temperature scale on scientific grounds. In his Swedish paper "Observations of two persistent degrees on a thermometer" he reports on experiments to check that the freezing point is independent of latitude (and also of atmospheric pressure!). He determined the dependence of the boiling of water with atmospheric pressure (in excellent agreement with modern data). He further gave a rule for the determination of the boiling point if the barometric pressure deviates from a certain standard pressure.
http://www.astro.uu.se/history/celsius_scale.html
Metric Units for Volume
Kiloliter kL 1000 Liter
Hectoliter hL 100 Liter
Dekaliter daL 10 Liter
Liter L 1 Liter
Deciliter dL 1/10 Liter
Centiliter cL 1/100 Liter
Mililiter mL 1/1000 Liter
Metric Units for Length
Kilometer km 1000 meters
Hectometer hm 100 meters
Dekameter dam 10 meters
Meter m 1 meter
Decimeter dm 1/10 meters
Centimeter cm 1/100 meters
Milimeter mm 1/1000 meters
English units
The English unit system was developed from a number of nonstandard units of measure. The inch was the length of 3 grains of barley placed end to end. The foot was the lenght of a human foot and a yard was the distance from the nose to the thumb of an outstreached hand. This was established by King Henry I of England.
Mass
English Units for Weight
Ounce oz 1/16 pound
Pound lb 16 ounces
Ton tn 2000 pounds
Temperature
The Fahrenheit scale, which measures temperature, was created by Daniel Gabriel Fahrenheit (1686-1736), a German-Dutch scientist, in 1724. Fahrenheit, who devoted much of his life’s work to the measurement of temperature, also invented the alcohol and mercury thermometers. On the Fahrenheit scale, the point at which frozen water melts is 32°, and the point where at which it boils is 212°. Between these two points is exactly 180°, a number easily divisible on a thermostat. Although we know with a degree of certainty what measurements Fahrenheit used to determine his scale, his process of arriving at the final scale is largely unknown.
Several stories have circulated regarding how Fahrenheit devised his scale. One is that he established 0° as the coldest temperature he could measure outdoors during the winter of 1708 to 1709 in Danzig (Gdańsk), Poland. This measurement and Fahrenheit's own body temperature, which he measured at 100°, were the two marks on which he based the rest of his scale. Many think that either his thermometer was off or he was running a fever that day, resulting in the relatively high reading on the bodily temperature. The scale was then divided into 12 separate segments, which were later divided into eight, creating a scale of 96 separate degrees.
http://www.wisegeek.com/what-is-the-history-of-the-fahrenheit-scale.htm
Volume
English Units for Volume
Ounce oz 1/8 cup
Cup c 8 ounces
Pint pt 2 Cups
Quart qt 2 pints
Gallon gal 4 quarts
Length
English Units for Length
Inch in 1/12 foot
Foot ft 12 inches
Yard yd 3 feet
Mile mi 5280 feet
Nonstandard units
of length
Seeds and precious stones
Parts of the body
Hand
Horses are measured in "hands" still today
Foot
Cubit
Cubit is the distance from a man's elbow to the tip of his longest finger.
Span
A span is the distance between the little finger and thumb when the hand is fully spread out.