par Rachel Yang Il y a 4 années
227
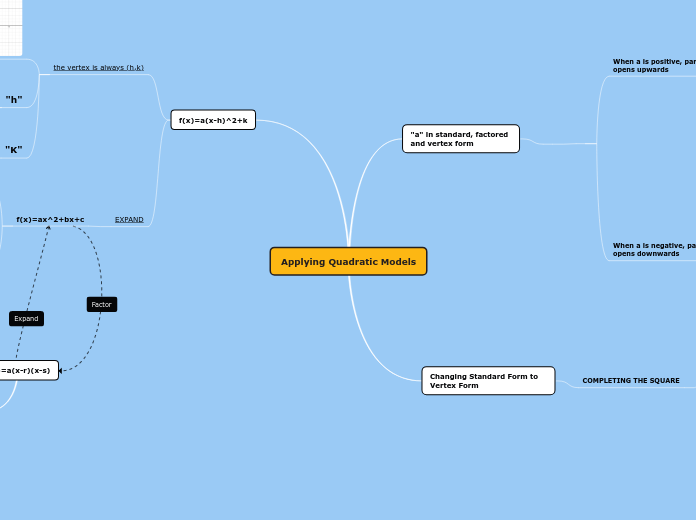
Applying Quadratic Models
Quadratic functions can be expressed in different forms, each highlighting unique characteristics of the parabola they describe. The standard form, \( f(x) = ax^2 + bx + c \), emphasizes the y-intercept and the shape dictated by the coefficient \