MAT.105X 9.1

Mere som dette

MAT.116 Overview

af David Kedrowski

Kinematics and Dynamics

af Khubaib W

Multiple Equations

af Jackie Lindquist

Future Perfect and Future Continuous

af Lia Ventura

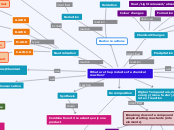
MAT.105X 9.1 Solving Absolute Value Equations

Solve an Equation of the Form |ax + b|=k for k<=0

k<0

For absolute value equations of the form |ax+b|=k where k<0, there is no solution, since the expression cannot be a negative distance from 0 on the number line.

k=0

For absolute value equations of the form |ax+b|=k, if k is 0 we only need to solve one equation, ax+b=0.

Solve an Equation of the Form |ax + b|=|cx + d|

If P and Q are expressions, then to solve |P|=|Q|, we rewrite the absolute value equation as the compound equation

P=Q or P=-Q

and solve for the variable.

If P and Q are expressions, then to solve |P|=|Q|, we rewrite the absolute value equation as the compound equation

P=Q or P=-Q

and solve for the variable.

That is, the equation will be true if the values of P and Q are the same or if they values of P and Q are opposites.

Solve an Equation of the Form |ax + b|+t=c

We need to get the absolute value expression by itself on one side of the equation (that is, we need to isolate the absolute value expression).

We need to do this so we can determine how far we're interested in that expression being from zero on a number line.

Solve an Equation of the Form |ax + b|=k for k>0

Solving

To solve an absolute value equation of the form |P|=k, where P represents some expression and k is a positive real number, we rewrite the equation as a compound equation.

P=k or P=-k

and then solve for the variable in P.

Understand the Meaning of an Absolute Value Equation

Absolute Value Equations

An absolute value equation, like |x|=6, asks the question

What numbers have a distance of 6 units from zero on a number line?

In this case there are two such numbers, -6 and +6.

That is, |-6|=6 and |6|=6.

Distance from Zero

The absolute value of a number is that number's distance from zero on a number line.

We take distance to be a nonnegative quantity.