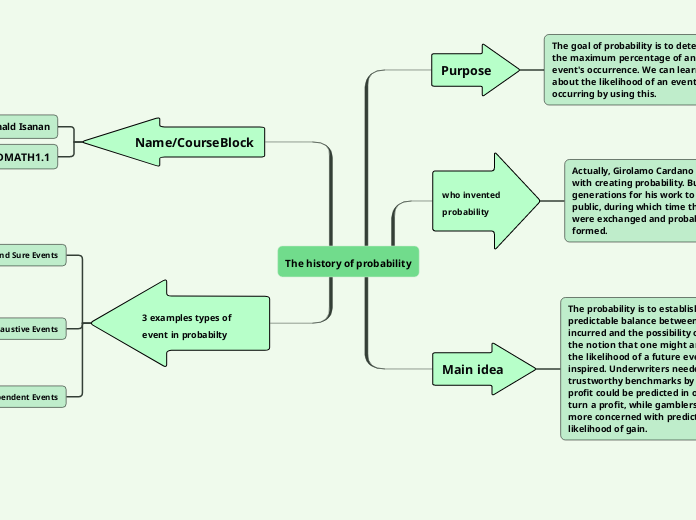
The goal of probability is to determine the maximum percentage of an event's occurrence. We can learn about the likelihood of an event occurring by using this.
Actually, Girolamo Cardano is credited with creating probability. But it took generations for his work to be made public, during which time the letters were exchanged and probability was formed.
The persons who develop probabilty
Pierre de Fermat (1623–1662) and Blaise Pascal (1601-1665). Blaise Pascal and Pierre de Fermat are recognized as the fathers of probability since they created the foundation for the field by thinking through a gambling issue given by Chevalier de Mere in 1654. The question concerned the number of rolls needed to guarantee getting a six on a two-dice roll.
The probability is to establish a predictable balance between the risks incurred and the possibility of benefit, the notion that one might anticipate the likelihood of a future event was inspired. Underwriters needed trustworthy benchmarks by which a profit could be predicted in order to turn a profit, while gamblers were more concerned with predicting the likelihood of gain.
Lara, Reynald Isanan
BSEDMATH1.1
Impossible and Sure Events
If the probability of occurrence of an event is zero, it is referred to as an impossible event; if the probability of occurrence of an event is one, it is referred to as a sure event. In other words, the empty set is an impossible event, whereas the sample space S is a foregone conclusion.
Exhaustive Events
If all of the events in a set consume the entire sample space, the set is said to be exhaustive.
Independent Events and Dependent Events
If the occurrence of one event is completely unaffected by the occurrence of another, that event is referred to as an independent event in probability, while events that are affected by other events are referred to as dependent events.