Energía Potencial Elástica
¿Que es la energía potencial elástica ?
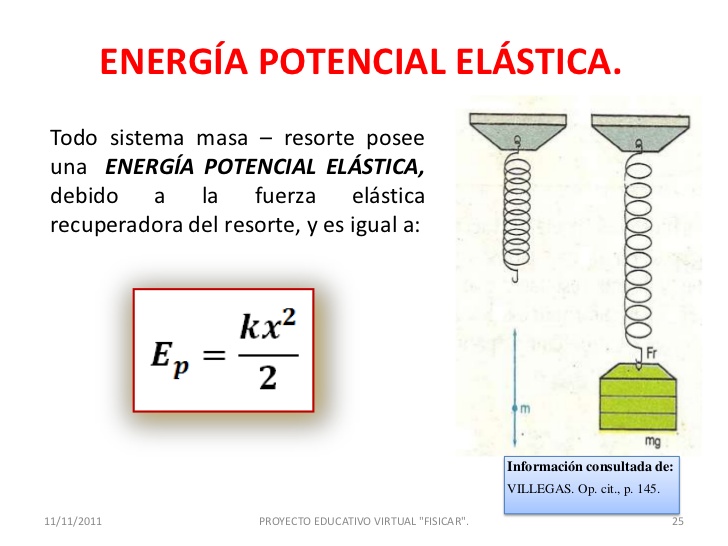
La energía potencial elástica es energía almacenada que resulta de aplicar una fuerza para deformar un objeto elástico. La energía queda almacenada hasta que se quita la fuerza y el objeto elástico regresa a su forma original, haciendo un trabajo en el proceso. La deformación puede implicar comprimir, estirar o retorcer el objeto. Muchos objetos están diseñados específicamente para almacenar energía potencial elástica, por ejemplo:
1.- El muelle de un reloj de cuerda.
2.-Un arquero que estira su arco.
3.-Un trampolín doblado justo antes de que el clavadista brinque.
4.-La liga de hule de una resortera.
5.-Una pelota de goma, comprimida en el momento en el que choca con una pared de ladrillos.
¿Cual es la formula para la energía potencial elástica ?
La relación entre la magnitud de la fuerza (F) y el cambio en la longitud del medio elástico (x) puede expresarse como:
F = K x
donde K es una constante que tiene un valor distinto para cada cuerpo elástico y es una medida de su rigidez. Entre más grande sea el valor de K, para un resorte por ejemplo, mayor fuerza habrá que aplicar para estirarlo o comprimir. FUENTE: http://www.cursosinea.conevyt.org.mx/cursos/cnaturales_v2/interface/main/recursos/antologia/cnant_2_08.htm
Anexos


Ejemplo

En una prueba experimental de alcance, un dardo de goma de 80,0 [g] es presionado contra un resorte. El resorte, de constante k= 250 [N/m], se comprime 5,00 [cm] y se libera. Si el dardo abandona el resorte cuando este alcanza su longitud natural, ¿qué rapidez adquiere el dardo? (Despreciar la fricción).
Cuando el resorte es comprimido por el dardo, la energía potencial que almacena será:
\[ Ep_{elas}=\frac{1}{2}kx^{2}=\frac{1}{2}(250N/m)(-5\cdot 10^{2} m)^{2} \]
\[ Ep_{elas}=0,313 [J] \]
Cuando el dardo se libera partiendo del reposo, la energía potencial elástica almacenada en el sistema se transforma en energía cinética (\frac{1}{2}mv^{2}) del dardo, por lo que, al despejar, la rapidez queda:
\[ V=\sqrt{\frac{2E_{k}}{m}}=\sqrt{\frac{2(0,313J)}{80\cdot 10^{-3} kg}} \]
\[ \boxed{ V=2,80[m/s] } \]
