Elementary Mathematics
Week 1
We started the class by going over the syllabus, future assignments, required books, and some class routines like math talk.
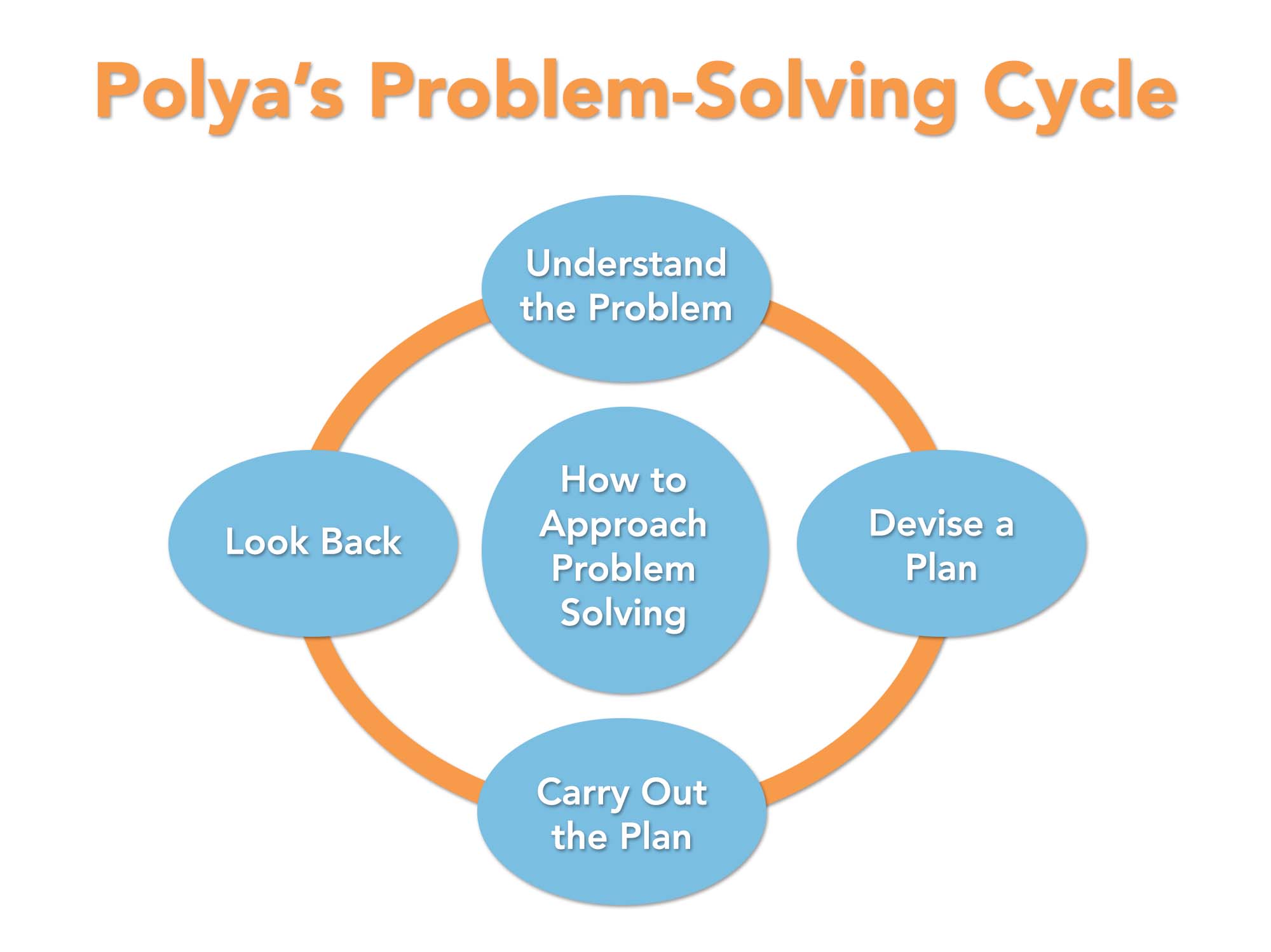
Polya's problem process
We were given a handout that explain Poyla's Problem-Solving Process. In Polya's Problem-Solving Process, we will understand the problem, devise a plan, carry out the plan, and look back. After we familiarized ourselves with Polya's Plan, we went over different scenarios where we had to go step by step over Polya's Process.
Intro to base ten and understanding place value.
We went over what are base 10 blocks. There are Ones (1), Longs (10), Flats (100), and Cube (1000). We learned their importance in the classroom which is to aide in understanding place value (the amount a number is worth). Then we watched a video from ASU that went over some of the first things a child learns in math which is 1- to-1 correspondence, cardinality, and subitizing.1-to-1 correspondence is when each number a child counts is toward an item they are counting. Cardinality is when they count something, and when asked again how much is it, they already know without counting because they already counted.Subitizing is when they look at something (like dice) and already know the amount without counting.
Week 10
Fractions
For week 10, we went into a brief introduction about fractions. What we were more focused on this week was creating a lesson using the state standards. I want to teach first grade and they aren't really learning about fractions. However, I came up with something easy for them to do following standard 1.NBT.B.3. I want students to think about which fraction is greater than, less than, or equal to another fraction.
Week 2

Number Sense With Adding & Subtracting
In this week we learned the basic understanding of what addition means, and how to show it to our students. Addition is combining two numbers together. 5+5=10How we show this is by using our knowledge of base ten. Show 5 ones + 5 ones and combine them to equal a long which has a value of 10.
Numbers in Different Bases
We know that 24 would equal 2 longs and 4 ones, but what if you were asked to show 24 in a different base like base 5? That is what we learned in week two as well. How to show numbers in different bases. Base 5 means that there are groups of 5 and you would need 5 ones to make a long, and 5 tens to make a flat. So, 24five would be 4 longs and 4 ones.
Week 9
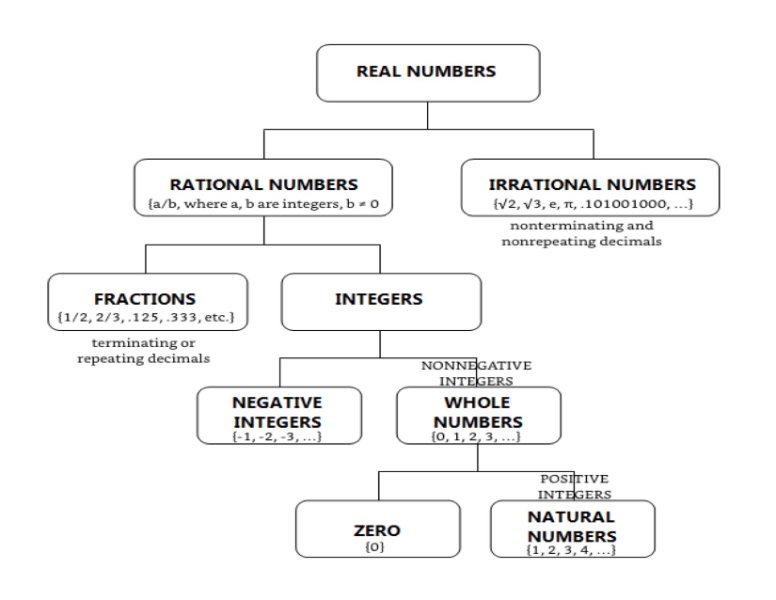
Integers
Integers are collections of whole numbers & negative numbers. However, this does not include fractions. Integers can be positive, negative, or a fraction but not zero.When trying to show integers you can use counters or the mini diagram. Counters: when using counters to show positive numbers use the yellow side and for negative numbers use the red side. Ex: to show 2-4 you would have 2 yellow counters and 4 red ones and the yellow ones would go on top, red on bottom. If you have a positive on top of a negative they cancel out. In our case 2 counters are lined up with each other so the remaining would be 2 red, making this problem's answer -2. Mini diagram: When using the mini diagram, you are just putting a positive (+) or negative (-) sign and putting them above the appropriate numbers. The larger number will get two signs. Ex: If I had 35+(-64), I would put one positive sign above 35, and two negative signs above 64. This helps the students easily see if their answer will be a positive or a negative number.
aRules of integers
Some rules to follow when working with integers are: pos+pos= posneg+neg= negpos+neg & neg+pos= using the sign of the larger absolute value number.
Exam #2
This exam went over what we have learned from week 5 to now.
Week 6
Showing multiplication and area model
In week 6 we learned how to show multiplication and an area model. We can show multiplication with our base ten blocks. The area model is a diagram used to solve multiplication problems in a box (Pictured in mind map).There are different strategies used when teaching multiplication:Time testProgress chartsFlashcardsTricksDepending on how you use the strategies they could be ineffective or effective. Most people dislike timed tests because of the stress, but they can increase automaticity when used correctly.
Order of multiplication facts
The multiplication facts should be taught 1's, 10's, and 5's first. Then 3's, 9's, and doubles. Lastly 4's 6's, and 8's. We also did two assignments on this called Multiplication and Automaticity and another creating an assignment we'd use in our future classroom following the guidelines of the state.
Week 11
Decimals
In week 11, we learned about decimals and how to add, subtract, and multiply them. A decimal is a number (based on the number 10) that contains a decimal point. Ex: 3.25To show how to add, subtract or multiply a decimal you can use base 10 blocks. However, it is a little different. A hundredth block is one unit, a long is a tenth (1/10 or 0.10), and a one is one hundred (1/100 or 0.01). Ex: 0.13 + 0.26 would have 3 tenths because 1 and 2 are in the tenth place and you are adding. Then, you would have 9 one-hundredths because 3 and 6 are in the one-hundredth place and you are adding.
a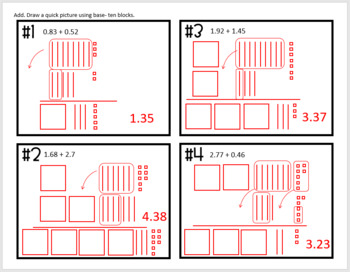
Addition

Subtraction

Multiplication
Week 5
Building Multiplication
We learned the basics of multiplication: 2*5 means you have 2 groups of five. To make it easier for our students to understand, you can show them how to build it in base ten. This is called an area model.
Week 7
Division
We learned about division and the best way to teach our students how to think about division. If we have 15/5 and put 15 into 5 groups equally. We also learned about long division. We use long division to divide larger numbers into small groups. The steps are multiply, subtract, and bring down. Two methods to use when doing long division are upwards division and repeated subtraction.
a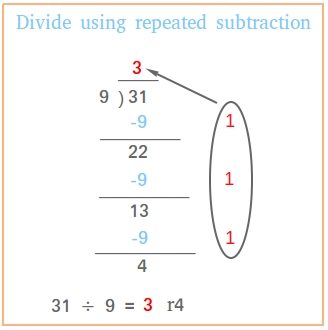
Repeated subtraction
Upwards division
We submitted our first part of the mind map (1-5)
Week 12

Order of operations
Order of operations is a series of steps to solving an equation. To help students remember these series of steps we use PEMDAS (Please Excuse My Dear Aunt Sally). P: parenthesisE: exponents M: multiplicationD: divisionA: additionS: subtractionFollowing these steps will help students break down big and complicated problems. Underlying each step can also help visual learners.
Week 4
Alternative Algorithms
We went over more algorithms to add. Expanded Form: Breaking down the number to add easier. For example, 25+13 would be 20+5 and 10+3. Left to right: In this method, you would add the two left numbers first then the last number to the right, and then find the sum of those numbers. 40+31 would be 4+3=70 and 0+1=1 then 70+1=71Lattice method: Stack the numbers you are adding on top of each other and then add a box underneath and then split the box in half from the right corner to the left. You use this method because carrying the number can be confusing for beginners.
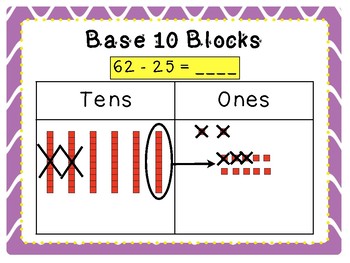
Showing Subtraction
To show subtraction you are drawing out your base ten models and show that you are taking an amount away by circling the amount and drawing an arrow out then counting the rest to find your total. This can be helpful for beginners especially when they run out of fingers to count.
Exam #1
This exam went over what we have learned from week 1 to now.
Week 8
Divisibility Rules
In week 8 we went over the rules for divisibility and why they are useful. You can use them in the classroom when testing a number to see if it is a multiple of another number or to check for prime numbers. I found a nice poster to use in the classroom as a reminder of the divisibility rules so I will let the picture do the explaining. All those numbers 2,3,4,5,6,8,9, and 10 will divide evenly with each other if they follow the rules listed in the picture. We also did an in-class activity/homework assignment with different numbers and had to determine which numbers they'd be divisible by.
Week 3
Converting Bases
We went over how to convert other bases to another base building off of our knowledge last week about learning how to show numbers in different bases. Say you need to convert 34five to base six, you first have to find the value of 34five, then change it to base 6. If it is in base six, you need six ones to create a long so you might have to break a long that you have in five to make your acquired number fit in the base you are converting it to.

Addition Algorithms
We got an introduction on three different addition algorithms. Traditional: Just adding regularly.Friendly/Trade-off: Friendly is trading off a number so that both numbers can end in zero. Trading off is adding an amount to make one number end in zero. Scratch Method: This method helps when you have multiple numbers you need to add. Stack the numbers on top of each other and start with the column to the right and once you reach 10, scratch off that number and put the remaining next to it. Do the same thing to the left column and you should have your answer.
Week 13

Scientific notation
In week 13, we went over scientific notation. We use scientific notation to easily write really large numbers or really small numbers. It is also used to measure the ocean. When showing a big number, the exponent will always be positive. Ex: 45,000= 4.5*10^4When showing small numbers, the exponent will be negative. Ex: 0.00076= 7.6*10^-4. Standard form: Standard form is the number as is. 45,000Scientific notation: Scientific notation is making the number easy to write. 4.5*10^4To put a number in scientific notation, you move the decimal to the left or right depending on where the decimal is.
Exam #3
Exam 3 went over decimals, order of operations, and scientific notation.