av David Kedrowski för 15 årar sedan
535
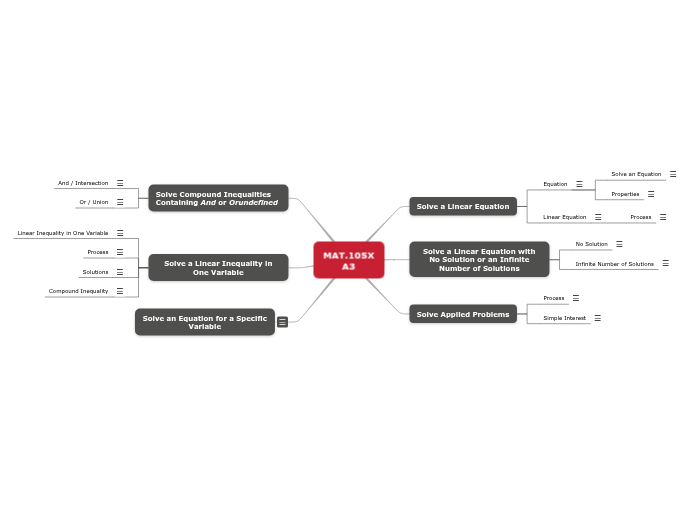
MAT.105X A3
av David Kedrowski för 15 årar sedan
535

Mer av detta
Treat all variables you are not solving for as constants.
Three parts: all operations must be performed on each of the three parts
Write in inequality notation
Graph on a number line
Write in set notation
Write in interval notation
The process is mostly the same as for solving linear equations in one variable. However,
when we multiply or divide both sides of the inequality by a negative number we must reverse the direction of the inequality symbol.
A linear inequality in one variable can be written in the form
ax+b<c,
ax+b<=c,
ax+b>c, or
ax+b>=c,
where a, b, and c are real numbers and a is not zero.
Take everything (but only take things that overlap once)
Take the overlap
I=PRT
I=interest earned (simple)
P=principal (initial amount invested)
R=annual interest rate (expressed as a decimal)
T=amount of time the money is invested (in years)
Read the problem carefully. Then read it again. Draw a picture, if applicable.
Identify what you are being asked to find. Define the variable; that is, assign a variable to the unknown quantity. Also,
Translate from English to math. Some suggestions for doing so are
Solve the equation.
Interpret the meaning of the solution as it relates to the problem. If there are other unknowns, find them. State the answer in a complete sentence. Be sure your answer makes sense in the context of the problem.
An equation has an infinite number of solutions if an identity results from the solution process.
We say the solution set is the set all real numbers.
An equation has no solution if a contradiction results from the solution process.
We say the solution set is the empty set.
A linear equation in one variable is an equation that can be written in the form ax+b=0 where a and b are real number and a is not zero.
An equation is a mathematical statement that two expressions are equal.
We can solve equations.
We can simplify expressions. Expressions do not contain an equal sign (=).
Let a, b, and c be real numbers.
To solve an equation means to find the value or values of the variable that make the equation true.