Measurement: Length, Area, & Volume

The Measurement Process
Starting the Process
Subtopic
The U.S. System of Measures
Units of Length
Units of Area
Units of Volume
Units of Capacity
Metric Units: The International System
The SI Decimal Prefixes
Metric Units of Length
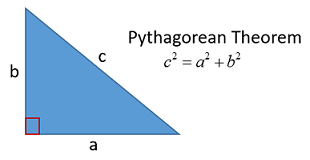
The Pythagorean Theorem
Area and Perimeter
Area
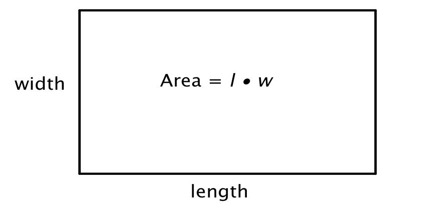
Area of a Rectangle

Area of a Parallelogram
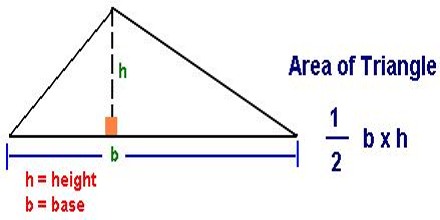
Area of a Triangle
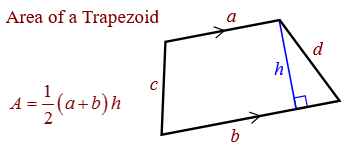
Area of a Trapezoid

Area of a Circle
Perimeter

The Circumference of a Circle
Volume
Volume of a Rectangular Box
Volume of a Right Prism or a Right Cylinder
Volume of a General Prism
Volume of a Pyramid or a Cone
Volume of a Sphere
Surface Area
Surface Area of a Right Prism or Right Cylinder
Surface Area of a Right Regular Pyramid
Surface Area of a Right Circular Cone
Surface Area of a Sphere
