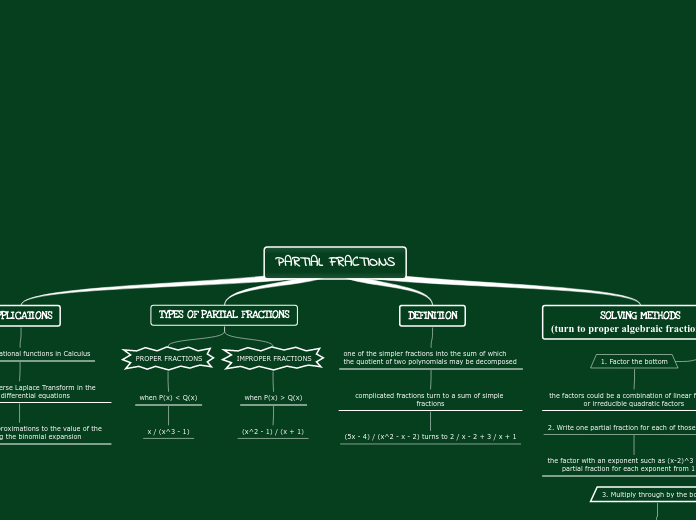
PARTIAL FRACTIONS
APPLICATIONS
1. Integrating rational functions in Calculus
2. Finding the Inverse Laplace Transform in the theory of differential equations
3. Able to make approximations to the value of the function using the binomial expansion
TYPES OF PARTIAL FRACTIONS
PROPER FRACTIONS
when P(x) < Q(x)
x / (x^3 - 1)
IMPROPER FRACTIONS
when P(x) > Q(x)
(x^2 - 1) / (x + 1)
DEFINITION
one of the simpler fractions into the sum of which the quotient of two polynomials may be decomposed
complicated fractions turn to a sum of simple fractions
(5x - 4) / (x^2 - x - 2) turns to 2 / x - 2 + 3 / x + 1
SOLVING METHODS
(turn to proper algebraic fractions first)
1. Factor the bottom
the factors could be a combination of linear factors or irreducible quadratic factors
2. Write one partial fraction for each of those factors
the factor with an exponent such as (x-2)^3 need a partial fraction for each exponent from 1 up
3. Multiply through by the bottom
so no longer have fractions
4. Now find the constants A1 and A2
making a system of linear equations (of each power) and solving
substituting zeros of the bottom