Трикутники

Трикутник – це геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з’єднують ці точки. Точки називають вершинами трикутника, а відрізки – його сторонами.
Види трикутників залежно від величини кутів

Залежно від величини кутів розрізняють:гострокутний - трикутник, у якого всі кути гострі.прямокутний - трикутник, у якого є прямий кут. тупокутний - трикутник, у якого є тупий кут.

Гострокутний

Прямокутний

Тупокутний
Види трикутників залежно від довжини сторін

Залежно від довжини сторін розрізняють:рівнобедрений - якщо дві сторони трикутника рівні, то його називають рівнобедренимрівносторонній - якщо всі сторони рівні, то його називають різносторонній - якщо всі сторони різної довжини, то його називають різностороннім.

Рівнобедрений

Рівностороніій

Різноcторонній
Ознаки рівностей трикутників

Ознаки рівності трикутниківЯкщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам та куту між ними іншого трикутника, то такі трикутники рівні.Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.

Перша ознака

Друга ознака

Третя ознака
Медіана, бісектриса та висота

Медіана трикутника – відрізок, який з'єднує вершину трикутника з серединою протилежної сторони.Для побудови медіани необхідно виконати такі дії: Знайти середину сторони. З'єднати точку, яка є серединою сторони трикутника, з протилежною вершиною трикутника. Це і буде медіана.Бісектриса трикутника - відрізок бісектриси кута трикутника, проведений від його вершини до протилежної сторони. Для побудови бісектриси необхідно виконати такі дії: Побудувати бісектрису кута трикутника (бісектриса кута — це промінь, що виходить із вершини кута й ділить його на дві рівні частини).Знайти точку перетину бісектриси кута трикутника з протилежною стороною.З'єднати вершину трикутника з точкою перетину бісектриси кута трикутника з протилежною стороною — цей відрізок і буде бісектрисою трикутника.Висота трикутника – перпендикуляр, проведений із вершини трикутника до прямої, що містить протилежну сторону.Для побудови висоти необхідно виконати такі дії: Провести пряму, яка містить одну зі сторін трикутника (у разі, якщо проводиться висота з вершини гострого кута в тупокутному трикутнику);Із вершини, що лежить навпроти проведеної прямої, опустити до неї перпендикуляр (перпендикуляр — це відрізок, проведений із точки до прямої, який утворює з нею кут величиною 90°). Це і буде висота.

Медіана

Бісектриса

Висота
Кути

ТеоремаСума кутів трикутника дорівнює 180°.Зовнішній кут трикутника - це кут, суміжний з внутрішнім. Внутрішніх кутів в трикутнику три, і їх сума дорівнює 180°. Суміжними кутами звуться кути, одна зі сторін яких лежить на одній прямій, а друга є спільною.Зовнішній кут трикутника дорівнює сумі внутрішіх, не суміжних з ним.
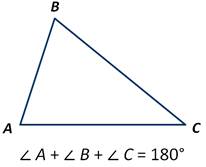
Сума кутів трикутника
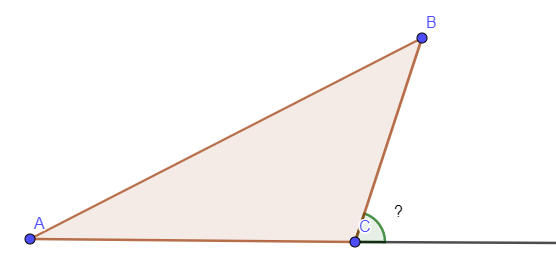
Зовнішній кут
Зовнішній кут трикутника та його властивості
Прямокутний трикутник
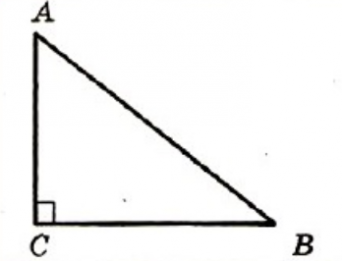
Якщо один з кутів трикутника прямий, то трикутник називається прямокутним. Сторона прямокутного трикутника, що лежить навпроти прямого кута, називається гіпотенузою, а дві інші – катетами.Властивості прямокутного трикутникаУ прямокутному трикутнику сума гострих кутів дорівнює 90°.Катет прямокутного трикутника, що лежить навпроти кута 30°, дорівнює половині гіпотенузи.Ознаки рівності прямокутних трикутниківОзнака рівності прямокутних трикутників за двома катетами. Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного трикутника, то такі трикутники рівні.Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом. Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.Ознака рівності прямокутних трикутників за катетом і протилежним кутом. Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.Ознака рівності прямокутних трикутників за гіпотенузою і гострим кутом. Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту другого прямокутного трикутника, то такі трикутники рівні.Ознака рівності прямокутних трикутників за гіпотенузою й катетом. Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого прямокутного трикутника, то такі трикутники рівні.
Сторони прямокутного трикутника
Прямокутний трикутник із кутом 30°
Пояснення та розв'язання задач
