ELEMENTI GEOMETRICI FONDAMENTALI

IL PUNTO
LA RETTA
E' COSTITUITA DA INFINITI PUNTI HA UNA SOLA DIMENSIONE: LA LUNGHEZZA; SI INDICA CON UNA LETTURA MINUSCOLA DELL'ALFABETO
PER DUE PUNTI DISTINTI (A, B), PASSA UNA SOLA RETTA
FRA DUE PUNTI QUALSIASI DI UNA RETTA SONO COMPRESI INFINITI PUNTI
LE PARTI DI UNA RETTA

SEMIRETTA
E' CIASCUNA DELLE DUE PARTI IN CUI UNA RETTA E' DIVISA DA UN SOLO PUNTO

SEGMENTO
CI POSSONO ESSERE DUE TIPI

SEGMENTI CONSECUTIVI
2 SEGMENTI CON UN ESTREMO IN COMUNE

SEGMENTI ADIACENTI
HANNO UN ESTREMO IN COMUNE, E SITROVANO DA PARTI OPPOSTE RISPETTO AL VERTICE IN COMUNE
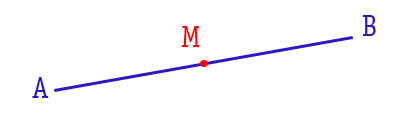
IL PUNTO MEDIO
IL PUNTO MEDIO E' IL PUNTO CHE DIVIDE IN 2 IL SEGMENTO IN 2 SEGMENTI CONGRUENTI
E' UNA FIGURA FORMATA DA 2 SEGEMNTI DISTINTI SU UNA RETTA A E B, E DAI PUNTI DELLA RETTA COMPRESA FRA A E B
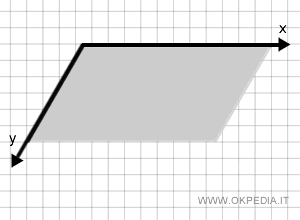
IL PIANO
E' COSTITUITO Da INFINITI PUNTI E INFINITE RETTE, HA DUE DIMENSIONI (LUNGHEZZE-LARGHEZZA), SI INDICA CON LETTERE DELL'ALFABETO GRECO
PER TRE PUNTI NON ALLINEATI PASSA UN SOLO PUNTO
PER UNA RETTA PASSANO INFINITI PIANI
PER UN PUNTO DI UN PIANO PASSANO INFINITE RETTE