EVOLUCIÓN HISTÓRICA DE LAS FRACCIONES Y EL NÚMERO CERO: ORIGEN, DESARROLLO Y RELEVANCIA DIDÁCTICA

Rama 1: Historia de las Fracciones

ORIGEN DE LAS FRACCIONES: Las fracciones surgieron de la necesidad de representar partes de un todo, especialmente en contextos comerciales y de distribución de recursos.

Egipto Antiguo (1800 a.C.):

Uso en agricultura y comercio: Los egipcios usaban fracciones para dividir tierras y alimentos, así como para realizar transacciones comerciales.

Fracciones unitarias: Principalmente usaban fracciones unitarias (con numerador 1). Por ejemplo, 1/2 se expresaba como una unidad dividida en dos partes iguales.

Escritura en jeroglíficos: Utilizaban símbolos jeroglíficos para representar fracciones.

Mesopotamia (Babilonios):

Sistema sexagesimal: Los babilonios empleaban un sistema basado en 60, que usaban para medir tiempo y ángulos, representando fracciones en ese contexto.

Impacto en la astronomía: Las fracciones sexagesimales fueron fundamentales para los avances astronómicos y la medición del tiempo, un legado que perdura hoy (60 minutos, 360 grados).

Grecia Antigua (300 a.C.):

Pitágoras y Euclides: Los griegos perfeccionaron la representación de las fracciones. Euclides definió las fracciones como relaciones entre números enteros, especialmente en su obra Los Elementos.

Fracciones como proporciones: Las fracciones se usaban principalmente para expresar proporciones geométricas y matemáticas.

Desarrollo de la Notación Moderna:

Edad Media (Siglo XII):

Matemáticos árabes: Al-Juarismi introdujo el concepto de fracciones decimales y mejoró las fracciones comunes. La numeración indoarábiga ayudó a la adopción de una notación más eficiente para las fracciones.

Leonardo de Pisa (Fibonacci): En su libro Liber Abaci (1202), Fibonacci introdujo a Europa la notación moderna de las fracciones (numerador y denominador separados por una línea).

Fracciones en la Didáctica Moderna:

Dificultades en la enseñanza: Las fracciones siguen siendo uno de los temas más complejos para los estudiantes debido a la abstracción del concepto y a las reglas especiales para operar con ellas (suma, resta, multiplicación y división).

Modelos visuales: Los diagramas de pastel, rectas numéricas y otros recursos visuales facilitan la comprensión de las fracciones como partes de un todo.

Aprendizaje significativo: En la educación moderna, se fomenta la aplicación de las fracciones en problemas reales, como la medición en cocina, construcción, y divisiones de grupos, para facilitar su comprensión práctica.

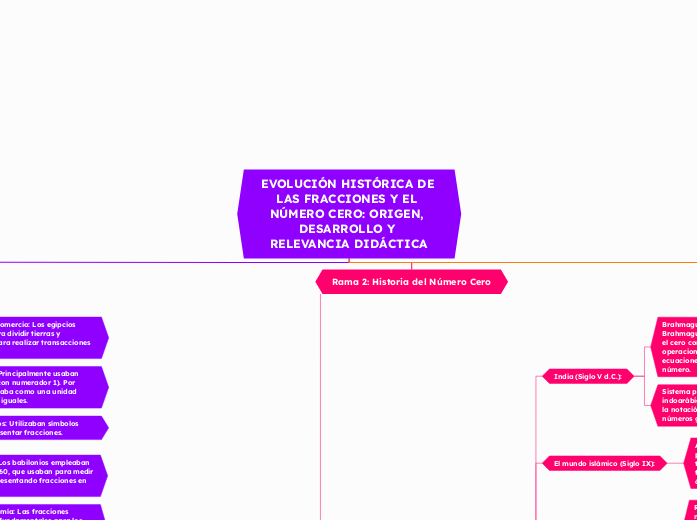
Rama 2: Historia del Número Cero

ORIGEN DEL NÚMERO CERO: El número cero tiene una historia fascinante, comenzando como un símbolo de "nada" y evolucionando hasta convertirse en un número esencial para el desarrollo del álgebra y el cálculo.

India (Siglo V d.C.):

Brahmagupta (628 d.C.): El matemático indio Brahmagupta fue uno de los primeros en definir el cero como un número que puede ser usado en operaciones aritméticas. Lo incorporó en las ecuaciones y lo trató como cualquier otro número.

Sistema posicional: En el sistema numérico indoarábigo, el cero ocupaba un lugar crucial en la notación posicional, permitiendo representar números grandes y pequeños con eficiencia.

El mundo islámico (Siglo IX):

Al-Juarismi y la difusión del cero: El matemático persa Al-Juarismi difundió el uso del cero a través de sus tratados, que llegaron a Europa y facilitaron el desarrollo de la aritmética y el álgebra.

Europa Medieval (Siglo XII):

Resistencia filosófica y religiosa: En la Europa medieval, el concepto de "nada" era problemático para las creencias filosóficas y religiosas. Sin embargo, su adopción fue gradual, hasta que Fibonacci lo incorporó en sus escritos matemáticos.

Cero en las finanzas: Eventualmente, el cero fue aceptado debido a su importancia en la contabilidad y el comercio.

Impacto del Cero en la Matemática Moderna:

Desarrollo del Álgebra y el Cálculo: El cero es fundamental en el álgebra para resolver ecuaciones (por ejemplo, ecuaciones cuadráticas) y es clave para el desarrollo del cálculo, como se ve en los conceptos de límites y derivadas.

Revolución en la Física y Astronomía: El cero permitió un avance en los cálculos científicos, facilitando las ecuaciones que describen la física moderna, incluida la teoría de la relatividad de Einstein.

Cero en la Didáctica Moderna:

Dificultades en la comprensión: Explicar el cero a los estudiantes puede ser complicado, debido a su dualidad como símbolo de "nada" y su rol como número en el sistema decimal.

Uso en contextos concretos: Se utilizan ejemplos concretos, como en la contabilidad (saldo cero), para enseñar el cero. Las rectas numéricas también son útiles para mostrar cómo el cero es un punto de referencia entre números negativos y positivos.

Rama 3: Estrategias Didácticas Modernas

Estrategias Didácticas para la Enseñanza de Fracciones y el Cero:

Materiales manipulativos: Los objetos físicos (como bloques de fracciones, fichas y tarjetas) ayudan a los estudiantes a visualizar y comprender las fracciones y el concepto del cero.

Uso de tecnologías: Programas interactivos y simulaciones en línea permiten a los estudiantes experimentar con fracciones y cero de manera dinámica.

Representaciones gráficas: Diagramas, gráficos y visualizaciones dinámicas apoyan la comprensión visual de los conceptos.

Contextos reales: Aplicaciones prácticas, como la división de alimentos o la representación del cero en situaciones cotidianas (temperaturas, dinero), ayudan a reforzar la importancia de estos conceptos en la vida diaria.

Mejoras en la Didáctica Moderna:

Interdisciplinariedad: Los conceptos de fracciones y cero se aplican en múltiples disciplinas, desde la física hasta la economía, lo que facilita su integración en diferentes áreas de conocimiento.

Fomento del pensamiento crítico: A través de la resolución de problemas y actividades colaborativas, se anima a los estudiantes a reflexionar sobre las aplicaciones más amplias de las fracciones y el cero en la matemática y la ciencia.