Tema 9. Funciones
1. Concepto de función
Representar gráficamente una función
Una función es una relación entre dos magnitudes, x e y, de forma que a cada valor x de la primera magnitud le corresponde un único valor y de la segunda
Así, x se denomina variable independiente e y es la variable dependiente.
3. Continuidad y puntos de corte con los ejes
Calcular los puntos de corte de una función

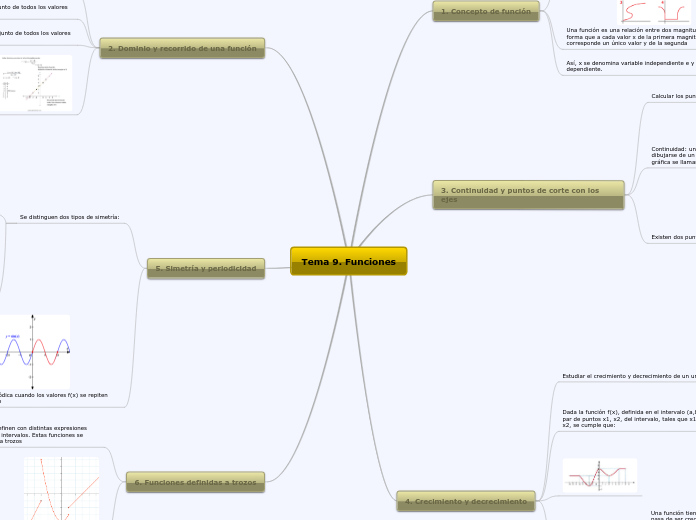
Continuidad: una función es continua si su gráfica puede dibujarse de un solo trazo. Los puntos donde se interrumpe la gráfica se llaman puntos de discontinuidad.
Existen dos puntos de corte:
Puntos de corte con el eje X, de la forma (a,0), donde el valor de a se calcula resolviendo la ecuación f(x)=0
Puntos de corte con el eje Y, de la forma (0,b), donde el valor de b se obtiene hallando f(0)

4. Crecimiento y decrecimiento
Estudiar el crecimiento y decrecimiento de un una función
Dada la función f(x), definida en el intervalo (a,b), si para todo par de puntos x1, x2, del intervalo, tales que x1 menor que x2, se cumple que:
x1 es menor que x2, la función es creciente.
x1 es mayor que x2, la función es decreciente
x1 es igual que x2, la función es constante
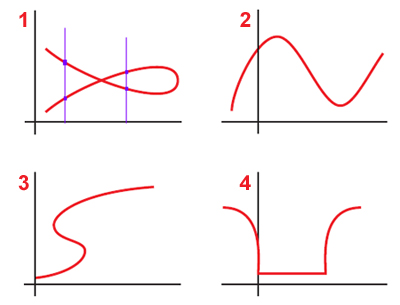
Máximos y mínimos:
Una función tiene un máximo relativo en x=a cuando un punto pasa de ser creciente a decreciente
Una función tiene un mínimo relativo si en x=a pasa de ser decreciente a creciente.
Subtema
2. Dominio y recorrido de una función
Calcular el dominio de una función
El dominio de una función es el conjunto de todos los valores que toma la variable independiente
El recorrido de una función es el conjunto de todos los valores que toma la variable dependiente

5. Simetría y periodicidad
Se distinguen dos tipos de simetría:

Función simétrica respecto del eje Y, cuando f(-x) 0 f(x). Este tipo de función se llama función par.
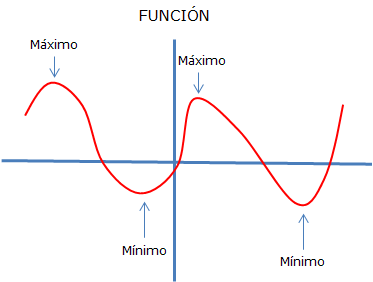
Función simétrica respecto respecto del origen, cuando f(-x) 0 f(x). Este tipo de función se llama función impar.

Una función es periódica cuando los valores f(x) se repiten cada cierto intervalo
La amplitud, T, del intervalo es el período, con k como número entero,
6. Funciones definidas a trozos
Existen funciones que se definen con distintas expresiones algebraicas para diferentes intervalos. Estas funciones se llaman funciones definidas a trozos
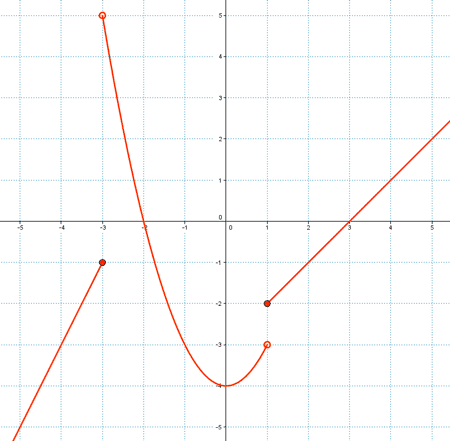
Subtema