Análisis de estructuras y Centroides y momentos de inercia WENDY VELANDIA

Armaduras

¿que son? Las armaduras son estructuras ligeras que sirven para salvar grandes claros en techumbres de naves industriales y puentes. sus elementos están unidos en sus extremos mediante articulaciones, por lo que solo trabajan a tensión o compresión no toman momento y las cargas están aplicadas en los nudos.

Tipos

pratt

Howe

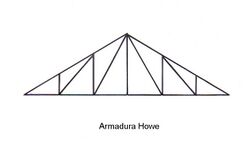
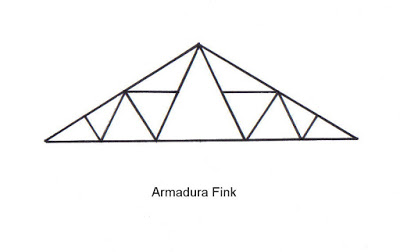
Fink

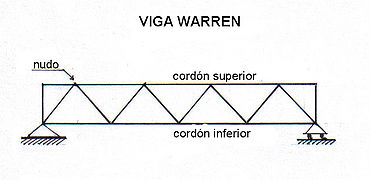
Warren

Baltimore

k

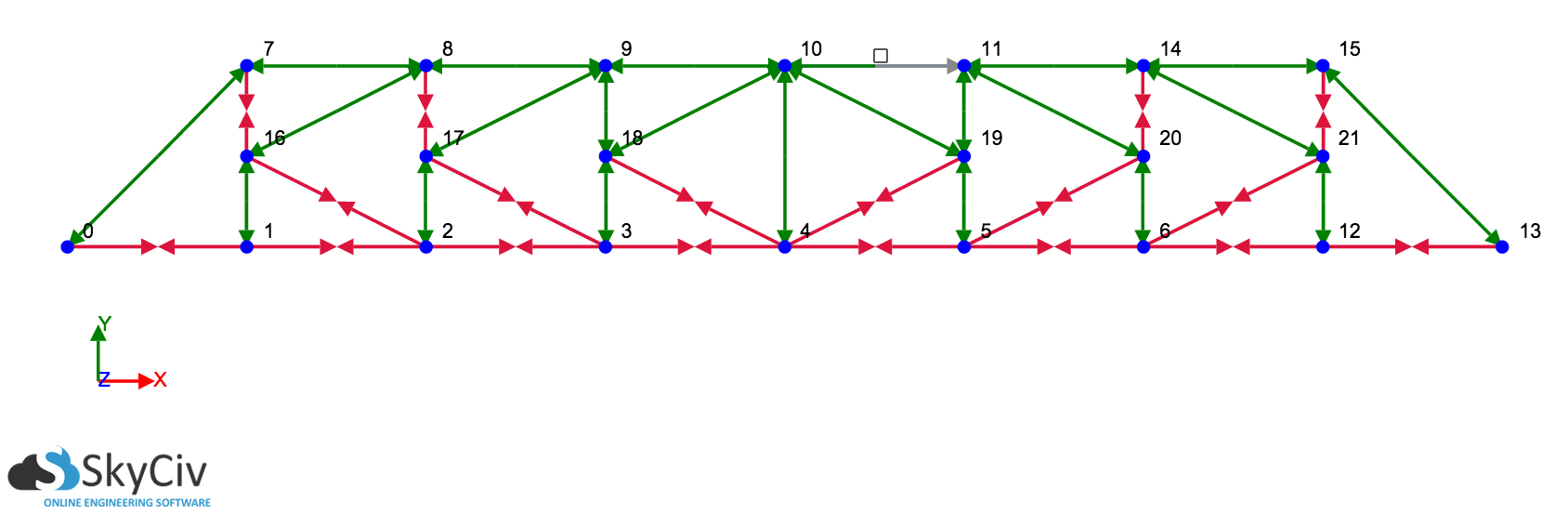
Método de nudos

El método de los nudos se usa para determinar las fuerzas de los miembros individuales en las armaduras estáticamente determinadas.
Cuando se aplica este método, cada nudo en la armadura se separa de los miembros conectados en un diagrama de cuerpo libre. Las fuerzas de los miembros se dibujan en el diagrama como flechas de vector que apuntan en dirección contraria al nudo,las fuerzas y cargas a las que estarán expuestas en su uso normal. Los tipos de armaduras más comunes incluyen armaduras planas, armaduras trianguladas y armaduras espaciales, que utilizan una combinación de barras y nodos para crear una estructura rígida y resistente^

Marco simple

Los marcos simples son elementos estructurales formados por trabes y columnas el eje longitudinal de este tipo de estructuras es una linea continua. En los puntos donde el eje cambia de dirección se conocen como nudos Esta estructura recibe el nombre de marco cuando su eje longitudinal está formado por lineas rectas El procedimiento de cálculo de los marcos es similar al de las vigas; esto es, primero se calculan las reacciones de los apoyos y luego se va seccionando el marco para obtener los diagramas de cortante y de momento en cada uno de los elementos que conforman el marco.

Momento de inercia de un área

• Primero. Cuanto mayor es la masa de un objeto, mas dificil es ponerlo en rotación o bien de tener su rotación alrededor de un eje Segundo. •El momento de inercia depende de la distribución de la masa del cuerpo rigido. Cuando mayor es la cistancia del centroide de la masa al eje, mayor será su momento de inercia

Momento polar de inercia

Aqui se utilizan las coordenadas polanes (p, en lugar de las rectangulares ix El momento polar de inercia queda definido como jo=jp dA

Centros de gravedad

Una característica general de todos los cuerpos rígidos es que poseen un peso, de acuerdo con el volumen y material del que están hechos. Su peso se encuentra distribuido en toda su volumen y se idealiza como un vector que apunta hacia el centro de la Tierra, debido a la fuerza de gravedad. Dicho vector tiene su punto de aplicación en el centroide del cuerpo rigido. Se dice que en este punto al cuerpo se encuentra on equilibrio, pues la suma de momentos alrededor de los ejes x, y ya es igual.

Centroides de áreas

Cuando se tienen areas simétricas, como el cuadrado, el rectángulo y el circulo, es muy fácil determinar su centroide, solo basta con encontrar la intersección entre sus ejes de simetria o dividir el área por la mitad en sentido vertical y horizontal.

Teorema de Steiner o de ejes paralelos

Consiste en transportar el momento de inercia de un área con respecto a un eje que pasa por su cen troide hacia un eje paralelo arbitrario, por medio de la siguiente expresión.

Producto de inercia

Se obtiene al integrar el producto de cada diferencial de área por las distancias normales x y y del centroide del área a los ejes coordenados centroidales Se calcula mediante la siguiente expresión:

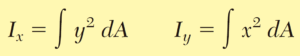
Método de las seleccines

Consiste en seccionar la armadura en el lugar donde se desean obtener las fuerzas de las barras Tiene como requisito cortar al menos tres barras en la misma sección. Una vez seccionada la armadura, se procede a encontrar el valor de las incógnitas mediante el equilibrio de la sección elegida.