Dinámica
DINÁMICA DEL MCU. FUERZA CENTRÍPETA
El movimiento circular y uniforme aplicado a un cuerpo es debido exclusivamente a una fuerza dirigida hacia el centro de la trayectoria circular,que se llama fuerza centrípeta o normal,Fc.
La segunda ley de Newton para el movimiento circular y uniforme se puede expresar así:
Fc=m·v^2/R o bien Fc=m·ω·R
En el movimiento circular y uniformemente acelerado la fuerza no está dirigida hacia el centro de la trayectoria circular.Su valor resulta de la suma de las componentes tangencial y centrípeta Ft y Fc.
-La fuerza centrípeta o normal,Fc,proporciona la aceleración normal necesaria para describir la circunstancia.
-La fuerza tangencial,Ft,hace que varíe el módulo de la velocidad,de forma que la trayectoria se recorre con velocidad creciente o decreciente.
La fuerza: F=√ (Fc^2+Ft^2)=m·R·√ (ω^4+α^2)
CANTIDAD DE MOVIMIENTO. REFORMULACIÓN LEYES DE NEWTON
La cantidad de movimiento o momento lineal es una magnitud vectorial que relaciona la masa y velocidad de un cuerpo de la siguiente forma:
p→=m⋅v→
Donde:
p→: Es el momento lineal. Su unidad de medida en el Sistema Internacional (S.I.) es el kg·m/s .
m : Es la masa del cuerpo. Su unidad de medida en el S.I. es el kilogramo ( kg )
v→: Es la velocidad del cuerpo. Su unidad de medida en el S.I. es el metro por segundo ( m/s )
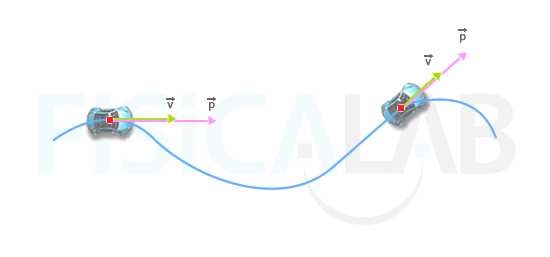
En la figura puedes observar, en azul, la trayectoria descrita por un coche. En verde, el vector velocidad es tangente a la trayectoria en cada punto. El vector cantidad de movimiento, en rosa, tiene igual dirección y sentido que la velocidad, pero distinto módulo.
No debes confundir el momento lineal de un cuerpo o una partícula con el momento de una fuerza.
CONSERVACIÓN MOMENTO LINEAL. CHOQUES
Cuando queremos estudiar varias partículas o cuerpos en conjunto, como si fueran uno solo, podemos decir que todos ellos forman un sistema de partículas.
El momento lineal o cantidad de movimiento de un sistema formado por n partículas es la suma de los momentos lineales de cada una de ellas.
p→=p→1+p→2+...+p→n
Donde:
p→: Es el momento lineal del sistema. Su unidad de medida en el Sistema Internacional (S.I.) es el kg·m/s
p→1, p→2, …,p→n: Son los momentos lineales de cada una de las partículas que componen el sistema (denotadas por los subíndices 1, 2, etc). Al igual que el momento lineal, su unidad de medida en el Sistema Internacional (S.I.) es el kg·m/s
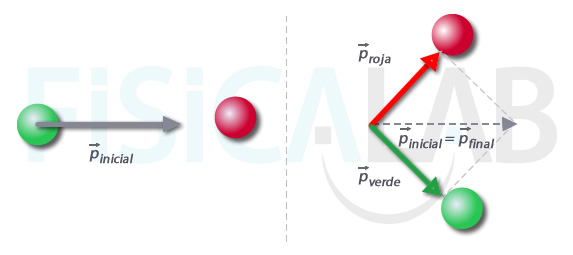
Conservación momento en choque
Si al lanzar la bola verde contra la roja, esta última adquiere el momento lineal p→roja, la única posibilidad es que la bola verde salga disparada en la dirección que marca la imagen, y con el momento lineal p→verde. Esto es debido a que el momento lineal final del sistema, que es la suma vectorial ( regla del paralelogramo ) de los momentos lineales de cada una de las bolas, debe coincidir con el momento lineal inicial, anterior al choque, que es el que tenía la bola verde.
p→antes=p→despues
She is the prettiest princess.
Create sentences
IMPULSO MECÁNICO. APLICACIONES
El impulso mecánico es la magnitud que nos permite cuantificar estas ideas.
Itself, Himself
Create sentences

Portero dando impulso al balón
El portero de la figura desplaza el brazo hacia atrás lo máximo posible para comenzar a realizar un movimiento hacia delante que le permita aplicarle la fuerza al balón durante más tiempo. Esto hará que llegue más lejos.
This, These
Create sentences
El impulso mecánico, de una fuerza , es una magnitud vectorial que relaciona dicha fuerza con el tiempo que dura su actuación.
I→=F→⋅Δt
Donde:
I→: Es el impulso mecánico de la fuerza. Su unidad en el Sistema Internacional (S.I.) es el newton por segundo ( N·s )
F→: Es la fuerza que estamos considerando, supuesta constante. Su unidad de medida en el S.I. es el newton ( N )
Δt: Es el intervalo de tiempo durante el cual actúa la fuerza. Su unidad de medida en el S.I. es el segundo ( s )
INTRODUCCIÓN : LEYES DE NEWTON
PRIMERA LEY
La ley de la inercia o primera ley postula que un cuerpo permanecerá en reposo o en movimiento recto con una velocidad constante, a menos que se aplique una fuerza externa.
Dicho de otro modo, no es posible que un cuerpo cambie su estado inicial (sea de reposo o movimiento) a menos que intervengan una o varias fuerzas.
La fórmula de la primera ley de Newton es:
Σ F = 0 ↔ dv/dt = 0
Si la fuerza neta (Σ F) aplicada sobre un cuerpo es igual a cero, la aceleración del cuerpo, resultante de la división entre velocidad y tiempo (dv/dt), también será igual a cero.
SEGUNDA LEY
La ley fundamental de la dinámica, segunda ley de Newton o ley fundamental postula que la fuerza neta que es aplicada sobre un cuerpo es proporcional a la aceleración que adquiere en su trayectoria.
La fórmula de la segunda ley de Newton es:
F= m.a
En donde
F = fuerza neta
m = masa, expresada en Kg.
a = aceleración, expresada en m/s2 (metro por segundo al cuadrado).
TERCERA LEY
El postulado de la tercera ley de Newton dice que toda acción genera una reacción igual, pero en sentido opuesto.
La fórmula de ley de acción y reacción es:
F1-2 = F2-1
La fuerza del cuerpo 1 sobre el cuerpo 2 (F1-2), o fuerza de acción, es igual a la fuerza del cuerpo 2 sobre el cuerpo 1 (F2-1) , o fuerza de reacción. La fuerza de reacción tendrá la misma dirección y magnitud que la fuerza de acción, pero en sentido contrario a esta.
Un ejemplo de la tercera ley de Newton es cuando tenemos que mover un sofá, o cualquier objeto pesado. La fuerza de acción aplicada sobre el objeto hace que este se desplace, pero al mismo tiempo genera una fuerza de reacción en dirección opuesta que percibimos como una resistencia del objeto.
CUERPOS APOYADOS SOBRE SUPERFICIES. FUERZA DE ROZAMIENTO
-La fuerza de rozamiento entre dos cuerpos es proporcional a la fuerza normal que ejerce un cuerpo sobre el otro.
-La fuerza de rozamiento no depende del área de contacto de ambos cuerpos, aunque sí de la naturaleza de sus materiales.
-La fuerza de rozamiento no depende de la velocidad a la que se deslicen los cuerpos.
-La fuerza de rozamiento tiene sentido opuesto al movimiento (a la velocidad).
Partiendo de estos factores, matemáticamente la fuerza de rozamiento se obtiene por medio de la siguiente expresión:
F→r=−μ⋅N⋅u→v
donde:
F→r es la fuerza de rozamiento.
μ es el coeficiente de rozamiento. Se trata de un valor adimensional que depende de la naturaleza y del tratamiento de las sustancias que están en contacto.
N es el módulo de la fuerza normal.
u→v es un vector unitario en la dirección y sentido del vector velocidad.
Observando la ecuación anterior, podemos concluir que su módulo es:
Fr=μ⋅N
Aunque podamos pensar que la fuerza de rozamiento es única, en realidad podemos distinguir dos tipos. Para entenderlo lo ilustraremos con un ejemplo.
Imagina que comienzas a empujar un cuerpo y no consigues moverlo. A medida que comienzas a aumentar la fuerza que aplicas el cuerpo comienza a deslizar. Por tanto, podemos distinguir dos fases, una que se produce antes de empezar a moverse y otra cuando se encuentra en movimiento.
En la primera fase, aunque aplicas la fuerza, este no se mueve. Si no se mueve, la resultante de las fuerzas que se aplican son nulas o lo que es lo mismo, la fuerza que aplicas y la fuerza de rozamiento se anulan:
F→=−F→r
En la segunda fase, el cuerpo comienza a deslizarse y la fuerza necesaria para mantenerlo en movimiento es menor que la que se necesita para iniciarlo.
Por tanto, se distinguen dos tipos de fuerza de rozamiento por deslizamiento: la fuerza de rozamiento estática (Fre) y que se ejerce mientras el cuerpo se encuentra bajo la acción de una fuerza que no le confiere movimiento y la fuerza de rozamiento dinámica (Frc) que se ejerce cuando el cuerpo se encuentra en movimiento. En cualquier caso se cumple que:
Frc<Fre(max)
donde:
Fre(max)=μe⋅NFrc=μc⋅N
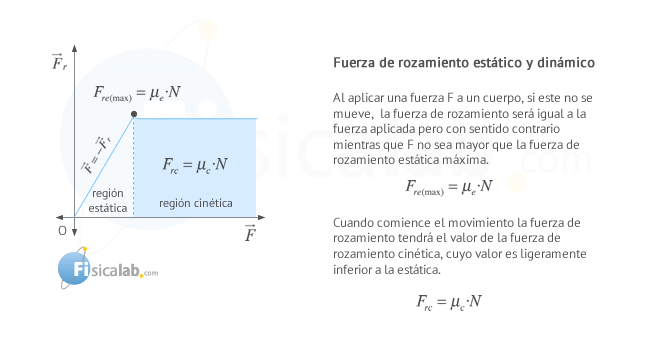
μc<μe
DINÁMICA DE CUERPOS LIGADOS , TENSIÓN ENTRE CUERPOS ENTRELAZADOS
La tensión,T,es una fuerza dirigida en la dirección de la cuerda,y su sentido dirigido alejándose del cuerpo.
-La tensión es una fuerza que se ha de sumar con las demás fuerzas que intervienen en el problema:
∑F=T+P
Denominaremos tensión a la fuerza de interacción ejercida entre dos cuerpos cuando uno de ellos transmite un movimiento a otro mediante un dispositivo material. Esta tensión se representará por T y se trata de una fuerza de acción-reacción sobre el intermediario, normamente una cuerda o cable.
Prepositions
La ley de Hooke establece que el alargamiento de un muelle es directamente proporcional al módulo de la fuerza que se le aplique, siempre y cuando no se deforme permanentemente dicho muelle.
F=k⋅(x−x0)
donde:
F es el módulo de la fuerza que se aplica sobre el muelle.
k es la constante elástica del muelle, que relaciona fuerza y alargamiento. Cuanto mayor es su valor más trabajo costará estirar el muelle. Depende del muelle, de tal forma que cada uno tendrá la suya propia.
x0 es la longitud del muelle sin aplicar la fuerza.
x es la longitud del muelle con la fuerza aplicada.
Si al aplicar la fuerza, deformamos permanentemente el muelle decimos que hemos superado su límite de elasticidad.
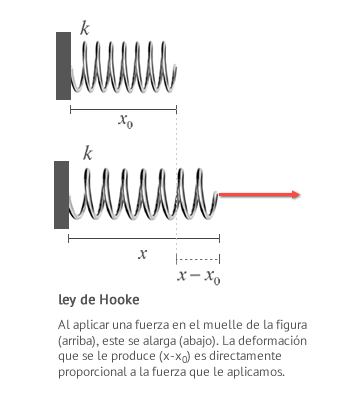
Cuando aplicas una fuerza a un muelle, probablemente este se alargará. Si duplicas la fuerza, el alargamiento también se duplicará. Esto es lo que se conoce como la ley de Hooke.
