🎲Probabilidad 🎲

Siendo n el numero los resultados que corresponden al evento Ay N cualquier resultado posible del experimento S

Si yo tengo un cajón con muchas pelotas con las que juega mi perro y, nuestro evento A es "sacar una pelota azul". En nuestro espacio muestral (que incluye todas las pelotas del cajón) del experimento S tenemos dos Pelotas azules en un total de siete pelotas. Asique:P(A) = 2/7Acá hay un video explicando el ejemplo:https://www.youtube.com/watch?v=xYco67hkECs

Siguendo con el ejemplo del cajón de pelotas. Si en este caso nuestro evento A sea "sacar una pelota azul o amarilla"Nuestro espacio muestral tiene 5 pelotas amarillas, 2 azules y 3 rojas. Dando un total de 10 pelotas.En este ejemplo los dos eventos son excluyentes ya que si saco una sola pelota que tiene un unico color, esta no podrá ser amarilla y azul al mismo tiempo.Entonces la probabilidad de nuestro evento a es:P(A) = 5/10 + 2/10 = 7/10

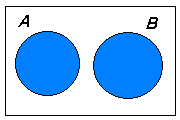
Cuando los eventos son no excluyentes y se quiere calcular la probabilidad. Cuando sumamos la prob, de A y la de B, estamos considerando dos veces la parte que se intersecta, por eso se resta una vez la intersección.

Si yo en un frasco tengo una mezcla de distintos tipos de dulces. Yo séque en el frasco hay 10 caramelos y 13 gomitas de menta.Y yo se que en el frasco hay 5 caramelos duros de frutilla, 3 caramelos masticables de naranja y 2 masticables de frutilla.Si mi evento A es :" Sacar un caramelo de frutilla"Y mi evento B es : "Sacar un caramelo masticable"La intesección de los eventos sería : "Sacar un caramelo de frutilla masticable"La probabilidad de la union de los eventos es:P(A U B): 7/23 + 5/23 -2/23 =10/23Hay que recordar que en el frsaco tambien habian gomitas de menta por eso la probabilidad nos queda dividido entre 23 posibles dulces.

Los eventos complementarios son un tipo de de eventos excluyentes, la unica diferencia es que la suma de sus probabilidades sería 1 ya que abarca todos los puntos muestrales del conjuno S, del cual tanto A como A´son subconjuntos.

Si yo tengo una bolsa que contiene 20 cararamelos de 3 sabores distintos: naranja frutilla y uva . Y tengo 10 de naranja, 4 de frutilla y 6 de uva.Si mi evento A es : "sacar un caramelo de frutilla", el evento A´será : "sacar un caramelo de naranja o de uva"entonces si yo quiero calcular la probabilidad de la suma de los dos eventos tengo:P(A) + P(A´)= 4/20 + 16/20 = 20/20 = 1

Probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B.

Se lee “la probabilidad de que ocurra B, dado que ocurrió A”P (B |A) =P (A ∩B )/P (A) siempre que P(A) > 0.

Dos eventos A y B son independientes si y sólo si P(B|A) = P(B) o P(A|B) = P(A)Esto se cumple si se asume la existencia de probabilidad condicional. De otra forma, A y B son dependientes.

P (A|B) = P (A ∩ B)/P (B) = 25/60 = 5/12= 0,4167 = 41,67 % 

A cada posible resultado del experimento, le hace corresponder un número

Toma valores dentro de un intervalo

Conjunto de valores que puede tomar la Variable Aleatoria "X" dentro de un Espacio muestral asignado para un Experimento.

La moda, que es el punto sobre el eje horizontal donde la curva es un máximo, ocurre en x = μ.La curva es simétrica alrededor de un eje vertical a través de la media μ.La curva tiene sus puntos de infl exión en x = μ ± σ, es cóncava hacia abajo si μ − σ < X < μ + σ, y es cóncava hacia arriba en cualquier otro caso.La curva normal se aproxima al eje horizontal de manera asintótica, conforme nos alejamos de la media en cualquier dirección.El área total 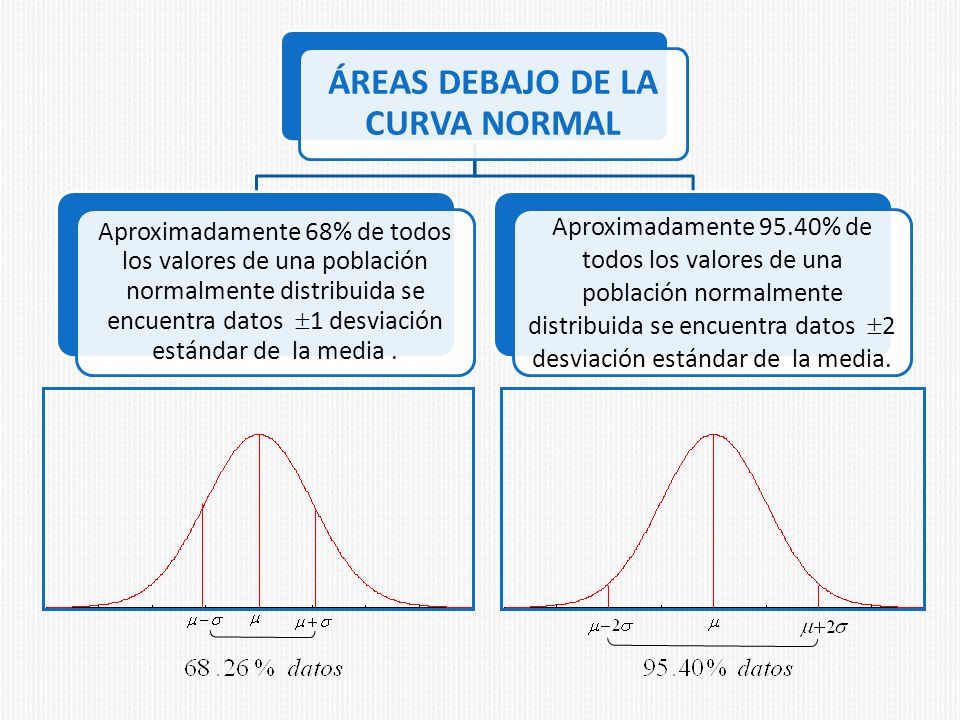bajo la curva y sobre el eje horizontal es igual a 1.

Tendencia de los valores de la v.a a agruparse en torno a un valor central o valor esperado

Cuando la variable aleatoria es discreta, la esperanza es igual a la suma de la probabilidad de cada posible  suceso aleatorio multiplicado por el valor de dicho suceso.f(x) es función de masa de probabilidad o función de densidad de probabilidad según corresponda.

Sea X una variable aleatoria con distribución de probabilidad f (x). El valor esperado de la variable aleatoria g(X) es...

Para una variable aleatoria absolutamente continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad f(x).

Sea X una variable aleatoria con distribución de probabilidad f (x). El valor esperado de la variable aleatoria g(X) es...

 Variabilidad de los valores de la v.a

Siendo f ( x) la función de masa de probabilidad o la función de densidad de probabilidad según corresponda