Натуральні числа.
Щоб полічити (порахувати) будь-які предмети, людей, тварин, використовують натуральні числа.Натуральні числа – це числа, якими користуються при лічбі: один, два, три, чотири, п’ять, шість, сім, вісім, дев’ять, десять, одинадцять, дванадцять і так далі. Такий ряд чисел називають ряд натуральних чисел.Зверніть увагу!ряд натуральних чисел починається з числа «один». «Один» — це найменше натуральне число;ряд натуральних чисел записують зазвичай у порядку зростання. Кожне наступне число, починаючи з другого, на один більше, ніж попереднє;ряд натуральних чисел нескінченний. Для будь-якого натурального числа можна назвати наступне, додавши до даного числа один. Отже, найбільшого натурального числа не існує.Щоб записати натуральні числа, використовують знаки, які називаються цифрами. Система запису чисел, якою ми користуємось, називається десятковою, оскільки вона містить десять цифр:1, 2, 3, 4, 5, 6, 7, 8, 9, 0.Запам’ятайте!Цифр – десять, натуральних чисел – безліч.У запису натуральних чисел відсутність одиниць якогось розряду показують цифрою «нуль». Цим знаком позначають також і число «нуль». Це число означає «жодного».
a
"Види чисел"
Натуральні числа поділяються на прості, складені та число 1.
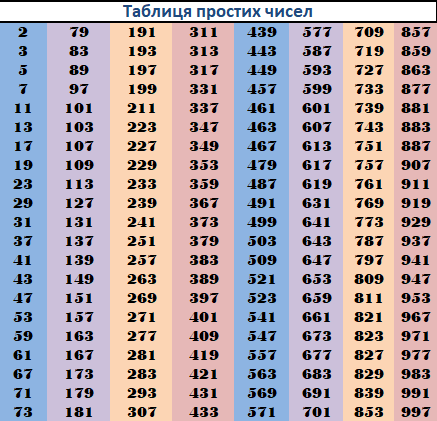
Прості числа
Натуральні числа, що мають тільки два дільники — одиницю і само себе , називають простими.Приклад. Числа 2; 3; 5; 7; 11 — прості, оскільки діляться тільки на 1 і самі на себе, тобто мають два дільники.

Складені числа
Натуральні числа, що мають більше двох дільників, називають складеними.Приклад. Числа 4; 6; 8; 10 — складені, оскільки діляться не тільки на 1 і самі на себе, а ще, наприклад, на 2, тобто мають більше двох дільників.Приклад. Число 48 — складене, оскільки, крім 1 і 48, воно ділиться, наприклад, ще на 2.

Число 1
Число 1 - особливе натуральне число, оскільки воно не належить ні до простих, ні до складених чисел.

Історія чисел
Натуральні числа — числа, що виникають природним чином при лічбі. Це числа: 1, 2, 3,4,… Множину натуральних чисел прийнято позначати знаком N Існують два основних підходи до означення натуральних чисел: числа, що використовуються при лічбі предметів (перший, другий, третій…) — підхід, загальноприйнятий у більшості країн світу; числа для позначення кількості предметів (відсутність предметів, один предмет, два предмети…) — підхід, прийнятий у роботах Ніколя Бурбакі, де натуральне число означається як потужність скінченних множин; Від'ємні та дробові числа не є натуральним числами.Як показують дослідження з історії математики, поняття натурального числа виникло на ранніх ступенях розвитку людського суспільства, коли у зв'язку з практичною діяльністю виникла потреба якось кількісно оцінювати сукупності. Найдавніші тексти - єгипетські папіруси і вавилонські клинописні таблички - свідчать про досить високу математичну культуру стародавніх єгиптян і вавилонян.Великим прогресом було винайдення цифр. Тепер стало можливим записати будь-яке число обмеженим набором символів. Наприклад, вавилоняни розвинули потужну позиційну систему, але зручнішою була індійська позиційна система числення, що дозволяла записати будь-яке натуральне число за допомогою десяти знаків — цифр; вона згодом стала всесвітньо визнаною і досі залишається такою. Таким чином, паралельно з розвитком писемності, поняття натурального числа приймає все більш абстрактну форму, відокремлену від будь-якої конкретності поняття числа, відтворюваного як у формі слів в усній мові, так і в формі позначення спеціальними знаками в письмі.Важливим кроком у розвитку поняття натурального числа є усвідомлення нескінченності натурального ряду чисел — потенційної можливості його безмежного продовження. Чітке уявлення про нескінченність натурального ряду відображене в пам'ятниках античної математики (III століття до н.е.), у працях Евкліда й Архімеда.Чітке означення поняття натурального числа на основі поняття множини було дано в 70-х роках XIX століття в роботах Георга Кантора. Спочатку він означує рівнопотужність множин. Потім число елементів однієї множини означається як те спільне, що має дана множина і будь-яка інша, рівнопотужна їй, незалежно від якісних особливостей елементів цих множин. Таке означення відображає суть натурального числа як результату лічби предметів. Нуль, спочатку означав відсутність числа; він став розглядатися як число лише після введення від'ємних чисел.

Вавилонська система числення
Ідея приписувати цифрам різні величини залежно від того, яку позицію вони займають у записі числа, уперше з’явилася в Прадавньому Вавилоні приблизно в III тисячоріччі до нашої ери.До нашого часу дійшли багато глиняних табличок Прадавнього Вавилону, на яких вирішені найскладніші завдання, такі як обчислення коріню, відшукання обсягу піраміди й ін. Для запису чисел вавилоняни використовували всього два знаки: клин вертикальний (одиниці) і клин горизонтальний (десятки). Усі числа від 1 до 59 записувалися за допомогою цих знаків, як у звичайній ієрогліфічній системі.Приклад:<< <<<<YYYYY = 45.Усі числа в цілому записувалися в позиційній системі числення з основою 60. Пояснимо це на прикладах.Запис YYYYYY YYY позначав 6 * 60 + 3 = 363, подібно тому як наш запис 63 позначає 6 * 10 + 3.Був у вавилонян і знак, що відіграв роль нуля. Їм позначали відсутність проміжних розрядів. Але відсутність молодших розрядів не позначалася ніяк. Так, число YYY могло позначати й 3 і 180 = 3 * 60 і 10 800 = 3 * 60 * 60 і так далі. Розрізняти такі числа можна було тільки за змістом.Відгомони цієї системи числення ми знаходимо в збереженому до наших днів звичаї ділити одну годину на 60 хвилин, одну хвилину на 60 секунд, повний кут — на 360 градусів.
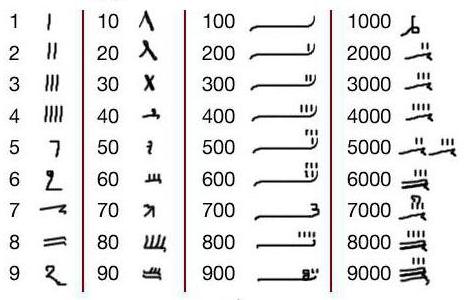
Єгипетська система числення
Єгипетська система числення — непозиційна система числення, яка вживалася в Стародавньому Єгипті аж до початку X ст. У цій системі цифрами були ієрогліфічні символи; вони позначали числа 1, 10, 100 і т. д. до мільйона.Числа, не кратні 10, записувалися шляхом повторення цих цифр. Кожна цифра могла повторюватися від одного до 9 разів. Наприклад, число 4622 позначалося так:****Фіксованого напрямки запису чисел не існувало: вони могли записуватися справа наліво або зліва направо і навіть вертикально. Наприклад: ієрогліфічний запис , та зворотний запис тих же ієрогліфів, позначали одне й теж число — «12».Однією з перших відомих згадок про єгипетські дроби є Математичний папірус Рінда. Три давніші тексти, в яких згадуються єгипетські дроби — це Єгипетський математичний шкіряний сувій, Московський математичний папірус і Дерев'яна табличка Ахміма. Папірус Рінда був написаний Ахмесон за доби Другого перехідного періоду; він включає таблицю єгипетських дробів для раціональних чисел виду 2 / n , а також 84 математичних задачі, їх вирішення і відповіді, записані у вигляді єгипетських дробів.Єгиптяни ставили ієрогліф( ер , « [один] з» або ре , рот) над числом для позначення одиничного дробу в звичайному запису, а у священних текстах використовували лінію. Наприклад: У них також були спеціальні символи для дробів 1 / 2, 2 / 3 і 3 / 4, якими можна було записувати також інші дроби (більші ніж 1 / 2).
a
Індо-арабська система числення
Ви будете здивовані, але арабські цифри вигадали в Індії. Історики вважають, що вони з'явилися в цій країні приблизно в 5 столітті. У цей час індійські філософи дійшли поняття нуля (шунья). Таким чином стався прорив у математиці, що дало можливість переходу до позиційної. числового запису.Індо-арабські та арабські цифри вважаються зміненими накресленнями найдавніших індійських цифр, які згодом були додані до арабського листа.Арабський учений Абу Джафар Мухаммад ібн Муса Аль-Хорезмі, був вражений перспективами, що відкриваються при використанні індійських цифр, і намагався всіма силами їх популяризувати. До речі, слово "алгебра" походить від назви знаменитої праці Абу Джафара "Китаб аль-джебр ва-ль-мукабала". Згодом учений написав твір, який назвав "Про індійський рахунок". Ця книга сприяла більшій популярності позиційної десяткової системи числового запису у всьому мусульманському світі, включаючи Іспанію.Першу згадку та накреслення арабських цифр (без нуля) в Європі можна виявити у Вігіланському кодексі. Спочатку ці цифри принесли маври до Іспанії приблизно 900 року.Всім людям із раннього дитинства знайомі цифри, за допомогою яких ведеться рахунок предметів. Їх лише десять: від 0 до 9. Тому і система обчислення називається десятковою. За допомогою них можна записати будь-яке число.Тисячоліттями люди застосовували свої пальці для позначення чисел. Сьогодні десяткова система використовується всюди: для вимірювання часу, при продажу та купівлі чогось, при різних розрахунках. Кожна людина має власні числа, наприклад, у паспорті, на кредитній картці.

НСК та НСД
Найбільший спільний дільник (НСД) — найбільше натуральне число, на яке без остачі ділиться кожне з даних. Наприклад, НСД(16,20,28)=4.Найменше спільне кратне (НСК) — найменше натуральне число, яке ділиться на кожне з даних чисел. Наприклад, НСК(2,3,4)=12.

Арифметичні дії
Над натуральними числами можна виконувати такі основні арифметичні дії: додавання, віднімання, множення та ділення. Також їх можна порівнювати, округлювати та підносити до степеня.
a
Вчені
Поняття натурального числа, викликане потребою лічби предметів, виникло ще в доісторичні часи. Процес формування поняття натурального числа тривав протягом усієї історії людства. На початковому етапі первісного суспільства поняття абстрактного числа не існувало. У свідомості первісної людини ще не сформувалося те спільне, що об'єднує наприклад, «три людини» та «три озера». Аналіз мов первісних народностей показує, що для лічби предметів різного типу використовувалися різні словесні обороти. Слово «три» в контекстах «три людини», «три човни» передавалося по-різному. Такі іменовані числові ряди були дуже короткими і завершувалися неіндивідуалізованим поняттями «багато», які також були іменованими, тобто висловлювалися різними словами для різних типів об'єктів, такими, як «натовп», «стадо», «купа» тощо.Спочатку числові терміни мали якісніший характер — відрізняли один, два та більшу кількість. Більші числа одержували додаванням. Наприклад, в австралійського племені ріки Муррей, 1 — енза, 2 — петчевал, 3 — петчевал-енза, 4 — петчевал-петчевал. Але навіть такі здібності людство здобуло після великого проміжку часу, в який користувалися лише з понять «один», «два» та «багато» (ще й досі збереглося плем'я, яке зупинилося на цьому етапові розвитку вмінь числового абстрагування).Джерелом виникнення поняття абстрактного числа була лічба предметів, що базувалася на зіставленні предметам даної сукупності предметів певної сукупності, що мала роль еталону. У більшості народів першим таким еталоном були пальці («лічба на пальцях»), що безпосередньо підтверджується мовознавчим аналізом назв перших чисел. На цьому етапі число стає абстрактним, незалежним від якості об'єктів лічби, але разом з тим пов'язаним з природою сукупності-еталону. Розширення потреб лічби спонукало людей користуватися з інших еталонів лічби, наприклад, зарубок на паличці. Для фіксації порівняно великих чисел стала використовуватися нова ідея: позначення деякого певного числа (у більшості народів — десяти) новим знаком, наприклад, зарубкою на іншій паличці.З розвитком писемності можливості відтворення чисел значно розширились. Спочатку числа стали позначати рисками на матеріалі, що слугував для запису (папірус, глиняні таблички тощо). Потім були введені інші знаки для великих чисел. Вавилонські клинописні позначення чисел, а також «римські цифри», що збереглися до наших днів, ясно свідчать саме про цей шлях формування позначень для чисел.Великим прогресом було винайдення «цифр». Тепер стало можливим записати будь-яке число обмеженим набором символів. Наприклад, вавилоняни розвинули потужну позиційну систему, що базувалася на цифрах 1 та 10, але фактично її основою було число 60. Зручнішою була індійська позиційна система числення, що дозволяла записати будь-яке натуральне число за допомогою десяти знаків — цифр; вона згодом стала всесвітньо визнаною і досі залишається такою (хоча форма цифр дещо змінювалася; цифри цієї системи ми називаємо арабськими, оскільки система прийшла в Європу через арабів). Таким чином, паралельно з розвитком писемності, поняття натурального числа приймає все більш абстрактну форму, відокремлену від будь-якої конкретності поняття числа, відтворюваного як у формі слів в усній мові, так і в формі позначення спеціальними знаками в письмовій.Важливим кроком у розвитку поняття натурального числа є усвідомлення нескінченності натурального ряду чисел — потенційної можливості його безмежного продовження. Чітке уявлення про нескінченність натурального ряду відображене в пам'ятниках античної математики (III століття до н.е.), у працях Евкліда й Архімеда. У «Началах» Евкліда встановлюється навіть нескінченність кількості простих чисел, а у книзі Архімеда «Псаміт» — принципи для побудови назв та позначень як завгодно великих чисел, зокрема більших за «число піщинок у світі».Питання про обґрунтованість поняття натурального числа довгий час у науці не ставилося. Поняття натурального числа настільки звичне і просте, що не виникало потреби в його означенні в термінах будь-яких простіших понять. Лише в середині XIX століття, під впливом розвитку аксіоматичного методу в математиці з одного боку, і критичного перегляду основ математичного аналізу — з іншого, назріла необхідність обґрунтування поняття кількісного натурального числа.Чітке означення поняття натурального числа на основі поняття множини було дано в 70-х роках XIX століття в роботах Георга Кантора. Спочатку він означує рівнопотужність множин. Потім число елементів однієї множини означається як те спільне, що має дана множина і будь-яка інша, рівнопотужна їй, незалежно від якісних особливостей елементів цих множин. Таке означення відображає суть натурального числа як результату лічби предметів.Інше обґрунтування поняття натурального числа базується на аналізі відношення порядку слідування, яке може бути задано за допомогою аксіом. Побудована на цьому принципі система аксіом була сформульована Джузеппе Пеано.

Евклід
Щоб знайти найбільший спільний дільник двох чисел, є дуже простий спосіб, відомий під назвою алгоритму Евкліда, або способу послідовного ділення.Алгоритм Евкліда, або алгоритм послідовного ділення, полягає ось у чому. Нехай дано натуральні числа a і b, a > b.Поділимо перше число на друге, дістанемо остачу r1 (r1 < b). Тепер b поділимо на r1, дістанемо остачу r2 (r2 < r1), далі поділимо r1 на r2 і т. д.Оскільки після кожного наступного кроку утворюється остача, менша від попередньої, то через скінченну кількість кроків дістанемо остачу, яка дорівнює нулю: ділення відбудеться націло і процес припиниться.Остання відмінна від нуля остача rk, на яку націло ділиться остача rk-1, буде найбільшим спільним дільником чисел a і b.Справді, запишемо сказане як ланцюжок рівностей:a = bq + r1,b = r1q1 + r2,r1 = r2q2 + r3,...rk-2 = rk-1qk-1 + rk,rk-1 = rkqk.З останньої рівності випливає, що rk є дільником rk-1, rk = (rk; rk-1). Через (n; т) позначено найбільший спільний дільник чисел n і m. З передостанньої рівності випливає, що rk ділить також rk-2 і rk = (rk-1; rk-2).Так, послідовно піднімаючись кроками вгору, дістанемо, що rk = (a; b).Приклад. Знайти НСД чисел 9765 і 6944.Розв'язання.9765 = 6944 · 1 + 2821,6944 = 2821 · 2 + 1302,2821 = 1302 · 2 + 217,1302 = 217 · 6.Відповідь. 217.

Архімед
Архімед (Archimedes) (близько 287 до н.е. — 212 до н.е., Сіракузи) — давньогрецький математик, фізик та інженер; один із найвидатніших вчених античності; обчислив площу сегмента параболи, поверхню та об’єм кулі, кульового сегмента й циліндра. Обчислив наближене значення числа “пі”, сформулював основні положення гідростатики, створив низку машин і споруд. У рік падіння Сіракуз Архімед загинув від руки римського солдата.

Ератосфен
“ Решето Ератосфена “ – спосіб складання таблиць простих чисел запропонований у ІІІ ст. до н.е. Ератосфеном. У стародавності писали на воскових табличках гострою паличкою - стилем. Тому Ератосфен, замість того щоб викреслювати написані їм на табличці числа, виколював їх гострим кінцем стилю. Після виколювання всіх складених чисел табличка нагадувала решето. З тих пір придуманий Ератосфеном метод відшукання простих чисел називають «решетом Ератосфена». Ось цей алгоритм:Виписав підряд усі натуральні числа від 2 до n.Залишав 2 і викреслював після нього всі числа через одне ( тобто парні числа: 4, 6, 8,…).Залишав число 3 і викреслював після нього всі числа через два ( тобто 6, 9, 12,…).Залишав число 5 і викреслював після нього всі числа через чотири (тобто 10, 15, 20,…) і т. д.При цьому деякі числа викреслювалися один і більше разів, а не закреслені числа виявилися прості.

"Дільники"та "кратні"
Якщо одне натуральне число ділиться націло на інше натуральне число,тоді перше число називають "кратним другого числа", а друге число — "дільником першого числа".