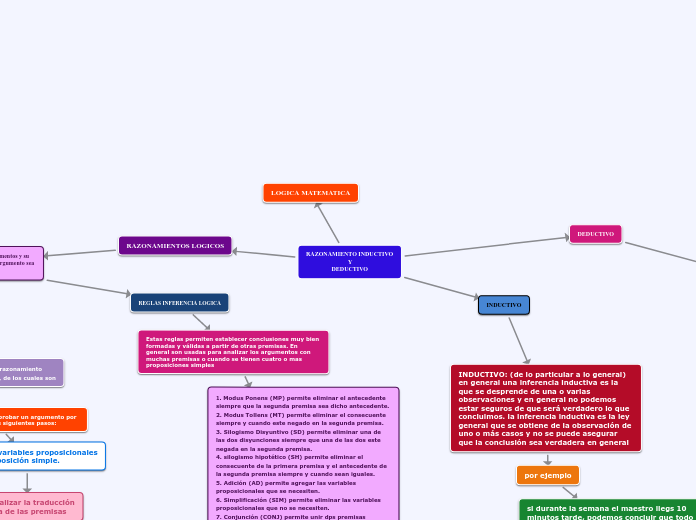
RAZONAMIENTO INDUCTIVO
Y
DEDUCTIVO

RAZONAMIENTOS LOGICOS

los razonamientos que estudia la logica se llaman argumentos y su tarea consiste en descubrir que es lo que hace que un argumento sea valido y constituya una inferencia correcta

REGLAS INFERENCIA LOGICA

Estas reglas permiten establecer conclusiones muy bien formadas y válidas a partir de otras premisas. En general son usadas para analizar los argumentos con muchas premisas o cuando se tienen cuatro o mas proposiciones simples

1. Modus Ponens (MP) permite eliminar el antecedente siempre que la segunda premisa sea dicho antecedente.
2. Modus Tollens (MT) permite eliminar el consecuente siempre y cuando este negado en la segunda premisa.
3. Silogismo Disyuntivo (SD) permite eliminar una de las dos disyunciones siempre que una de las dos este negada en la segunda premisa.
4. silogismo hipotético (SH) permite eliminar el consecuente de la primera premisa y el antecedente de la segunda premisa siempre y cuando sean iguales.
5. Adición (AD) permite agregar las variables proposicionales que se necesiten.
6. Simplificación (SIM) permite eliminar las variables proposicionales que no se necesiten.
7. Conjunción (CONJ) permite unir dps premisas diferentes.
8. Dilema constructivo (DC) permite eliminar los antecedentes de las dos condicionales dando como resultado la disyunción de los consecuentes.
9. Dilema destructivo (DD) permite eliminar los antecedentes de las dos condicionales, dando como resultado la disyunción de la negación de los consecuentes.
10. Absorción (ABS) permite reescribir el consecuente dando como resultado la conjunción del antecedente y consecuente.

validez de un razonamiento

para probar la validez de un razonamiento
tenemos diferentes métodos, de los cuales son

* uso de tabla de verdad para probar un argumento por tabla de verdad se efectúan los siguientes pasos:

1. Asignar variables proposicionales
a cada proposición simple.

2. Realizar la traducción
lógica de las premisas

3. Organizar el argumento, uniendo
las premisas con el operador logico.

4. OIbtener la cantidad de
combinaciones de valores de verdad.

5. Asignar los valores de verdad
a variables proposicionales.

6. Resolver las operaciones
lógicas.

LOGICA MATEMATICA

DEDUCTIVO

DEDUCTIVO: ( de lo general a lo particular)
cuando se conoce una ley general y se aplica a un caso particular. tambieb se conoce como inferencia deductiva cuando tenemos un caso que analiza todos los posibles resultados y de acuerdo a las premisas solo ahi una posible situación, en este casio decimos que la situación única es la clnclusión. cuando estamos seguros de qeu si las premisas son verdaderas entonces la conclusión también lo es.

por ejemplo

se sabe que siempre que llueve hay nubes, concluimos que el día de hoy que está lloviendo hay nubes, ya que en este ejemplo se analiza a todos los posibles resultados y de acuerdo a las premisas solo hay una posible situación, en este caso decimos que la situación única es la conclusión.

INDUCTIVO

INDUCTIVO: (de lo particular a lo general)
en general una inferencia inductiva es la que se desprende de una o varias observaciones y en general no podemos estar seguros de que será verdadero lo que concluimos. la inferencia inductiva es la ley general que se obtiene de la observación de uno o más casos y no se puede asegurar que la conclusión sea verdadera en general