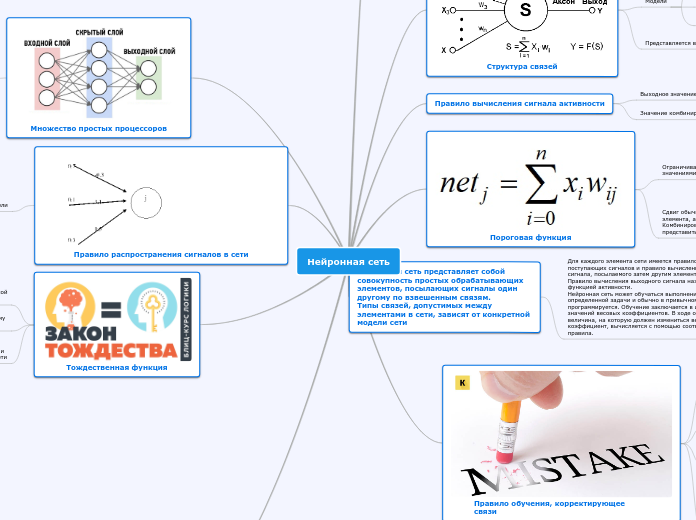
Нейронная сеть

Структура связей
Модели
Элемент,от которого исходит связь
Элемент,к которому данная связь направлена
Число, указывающее на весовой коэффициент
Представляется в виде матрицы W,с элементами i,j
Правило вычисления сигнала активности
Выходное значение - активность(представляется числом)
Значение комбинированного ввода - входное значение

Пороговая функция
Ограничивает активность
значениями 0 или 1
Чаще всего удобнее вычесть пороговое значение (называемое смещением или сдвигом) из значения комбинированного ввода и рассмотреть пороговую функцию в ее математически эквивалентной форме

Сдвиг w0 в данном случае оказывается отрицательным, а значение комбинированного ввода вычисляется по формуле
Сдвиг обычно интерпретируется как связь, исходящая от элемента, активность которого всегда равна 1 (рис. 9). Комбинированный ввод в данном случае можно представить в виде

Выходные элементы
Нейронная сеть представляет собой совокупность простых обрабатывающих элементов, посылающих сигналы один другому по взвешенным связям.
Типы связей, допустимых между элементами в сети, зависят от конкретной модели сети
Для каждого элемента сети имеется правило суммирования поступающих сигналов и правило вычисления выходного сигнала, посылаемого затем другим элементам сети. Правило вычисления выходного сигнала называется функцией активности.
Нейронная сеть может обучаться выполнению определенной задачи и обычно в привычном смысле не программируется. Обучение заключается в изменении значений весовых коэффициентов. В ходе обучения величина, на которую должен измениться весовой коэффициент, вычисляется с помощью соответствующего правила.

Правило обучения, корректирующее связи
Одно из главных преимуществ нейронных сетей заключается в том, что они предполагают наличие правил, с помощью которых сеть может программироваться автоматически.
Типичной формой обучения является управляемое обучение, когда для каждого набора данных, подающегося в процессе обучения на вход сети, соответствующий выходной набор известен.
Расхождение между тем, что даст сеть, и тем, что для данного учебного набора должно быть получено на самом деле, составляет ошибку, которая может использоваться для корректировки весов.
В процессе обучения на вход сети подаются образец за образцом, и в результате их обработки весовые коэффициенты корректируются до тех пор, пока для всех вводимых образцов ошибки не станут меньше некоторого приемлемого достаточно малого значения.
В завершение процесса сеть тестируется на данных, не представленных в фазе обучения: в результате можно оценить, насколько хорошо сеть работает с данными, которые в процессе обучения были ей неизвестны.

Множество простых процессоров
Входные сигналы
Весовой коэффициент

Правило распространения сигналов в сети
Модели
Правило обновления состояния элементов в сети
Результат комбинирования netj
Вводный элемент j
xi - выход элемента i
Число задействованных связей

Тождественная функция
Исходящий от входного элемента сигнал,должен быть такой
же,как и входящий
Входные элементы имею только по одному входному
значению
Данные от одного датчика
оказываются распределенными
между многими элементами сети
Сигмоидная функция

Выходные значения такой функции непрерывно заполняют диапазон от 0 до 1. Примером может служить логистическая функция,
Наклон и область выходных значений логистической функции могут быть разными. Например, для биполярного сигмоида областью выходных значений является диапазон между -1 и 1.


Модель сети показана на рис.11, и в данном случае это сеть с прямой связью, в которой имеются два входных элемента, два скрытых элемента и один выходной элемент. Прямая связь означает, что все связи могут идти только в направлении от входного слоя к выходному.
Скрытые элементы называются так потому, что они не получают данных от внешней среды непосредственно и не посылают данные непосредственно во внешнюю среду.
В данном случае в роли внешней среды можем выступать мы сами, подавая различные значения на вход сети (т е. входным элементам) и наблюдая результаты, полученные на ее выходе (т.е. на выходных элементах).
Элементы сети разделены по слоям:
входной слой содержит входные элементы,
скрытый слой — скрытые элементы,
выходной — выходные

Число элементов каждого слоя зависит от решаемой проблемы. Число входных элементов равно числу вводимых в структуру значений, а число выходных — числу значений, подаваемых данной структурой на выход. В нашем случае значение комбинированного ввода вычисляется по формуле

вывод получается как результат применения пороговой функции
В качестве вводимых данных рассмотрим первую пару значений ввода из табл.1, а именно пару значений [1,1]. Для первого скрытого элемента со смещением 1.5 получаем
net = (xo*1.5) + (x1*-1) + (x2*-1)
= (1*1.5)+ (1*-1) + (1*-1) = -0.5,
поэтому выходным значением элемента будет 0. Для второго скрытого элемента со смещением 0.5 получаем
net = (х0 * 0.5) + (х1* -1) + (х2 * -1)
= (1*0.5) + (1*-1) + (1*-1) = -1.5,
поэтому выходным значением элемента тоже будет 0. Для выходного элемента со смещением -0.5 получаем
net = (x0 *-0.5) + (x1 *1) + (х2*-1)
= (1* -0.5) + (0*-1) + (0*-1) = -0.5,
поэтому выходным значением будет 0. Если процедуру повторить для трех оставшихся пар, то мы увидим, что вывод указанной сети соответствует данным из последнего столбца табл. 1.