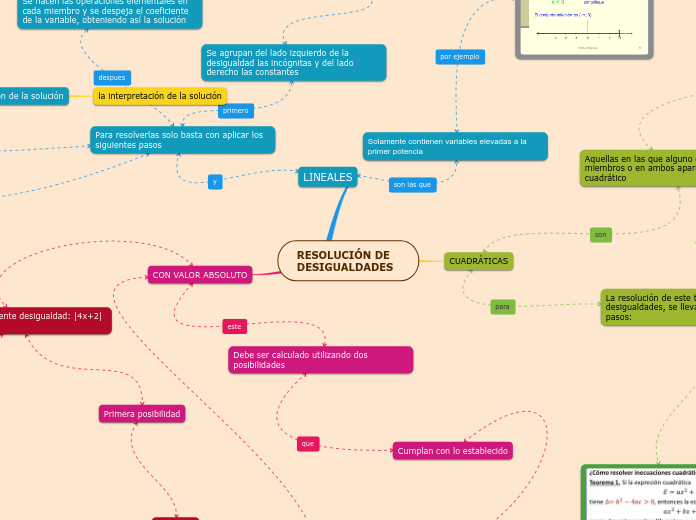
RESOLUCIÓN DE DESIGUALDADES
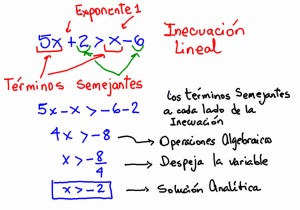
Solamente contienen variables elevadas a la primer potencia
Para resolverlas solo basta con aplicar los siguientes pasos
Se agrupan del lado izquierdo de la desigualdad las incógnitas y del lado derecho las constantes
Se hacen las operaciones elementales en cada miembro y se despeja el coeficiente de la variable, obteniendo así la solución
La interpretación de la solución
la interpretación de la solución
Son todos los números reales mayores que -1/3, la solución esta dada como un intervalo la cuál adopta la siguiente forma:
Aquellas en las que alguno de sus miembros o en ambos aparece un término cuadrático
La resolución de este tipo de desigualdades, se llevan los siguientes pasos:
Resolver la desigualdad: x2-3x+2 > 0
Se factoriza la desigualdad
(x-2)*(x-1) > 0
Las condiciones bajo las cuales la desigualdad aplicando para este caso la ley de los signos
(x-2)*(x-1) > 0
Se cumple si:
Primera condición: (x-2) > 0 y (x-1) > 0
Segunda condición: (x-2) < 0 y (x-1) < 0
Resolvemos las condiciones que hacen que se cumpla la desigualdad
(x–2) > 0 y (x–1) > 0
x > 2 y x > 1
La solución para este caso es x>2.
Ahora se resuelve la segunda condición
(x–2) < 0 y (x–1) < 0
x<2 y x<1
La solución pedida, que SIEMPRE se lee de izquierda a derecha, está dada por:
(x<1) U (x>2)
La solución expresada como un intervalo queda dada por:
Debe ser calculado utilizando dos posibilidades
Cumplan con lo establecido
Resuelva la siguiente desigualdad: |4x+2| > 6.
La solución para este caso seria:
4x+2 < -6
4x < -6-2
x < -8/4
x < -2
4x+2 > 6
4x > 6-2
x > 4/4
x > 1