FUNCTIONS
Distributive Property
how to solve expressions in the form of a(b + c)

Multiplying Polynomials
- To multiply two polynomials: multiply each term in one polynomial by each term in the other polynomial. add those answers together, and simplify if needed.
- simply foil out your factored terms by multiplying each term in one trinomial to each term in the other trinomial.
FOIL: first outer inner last

Create sentences
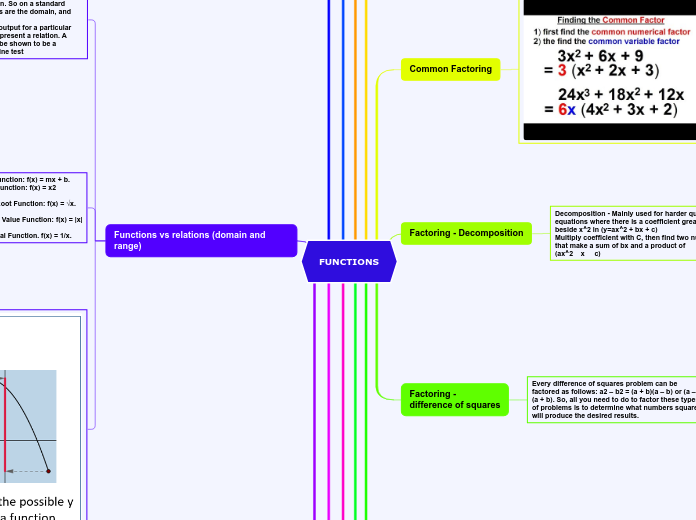
Common Factoring

Factoring - Decomposition
Decomposition - Mainly used for harder quadratic equations where there is a coefficient greater than 1 beside x^2 in (y=ax^2 + bx + c)
Multiply coefficient with C, then find two numbers that make a sum of bx and a product of
(ax^2 x c)

Create sentences
Factoring -
difference of squares
Every difference of squares problem can be factored as follows: a2 – b2 = (a + b)(a – b) or (a – b)(a + b). So, all you need to do to factor these types of problems is to determine what numbers squares will produce the desired results.

Create sentences
Factoring - perfect squares
Step 1: Factor out the GCF, if necessary.
Step 2:Write each term as a perfect cube.
Step 3: Identify the given variables.
Step 4:The terms of the binomial are the cube roots of the terms of the original polynomial

Simplifying rational expressions
Step 1: Factor both the numerator and denominator of the fraction.
Step 2: Reduce the fraction.
Step 3: Rewrite any remaining expressions in the numerator and denominator.
Step 4: Factor both the numerator and denominator of the fraction.

Combining Polynomials
you first need to identify the like terms in the polynomials and then combine them according to the correct integer operations. Since like terms must have the same exact variables raised to the same exact power

Function notation
simpler method of describing a function without a lengthy written explanation. The most frequently used function notation is f(x) which is read as “f” of “x”. In this case, the letter x, placed within the parentheses and the entire symbol f(x), stand for the domain set and range set respectively.

INVERSE FUNCTION

if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, i.e., g(y) = x if and only if f(x) = y. The inverse function of f is also denoted as f^{-1}.
Functions vs relations (domain and range)
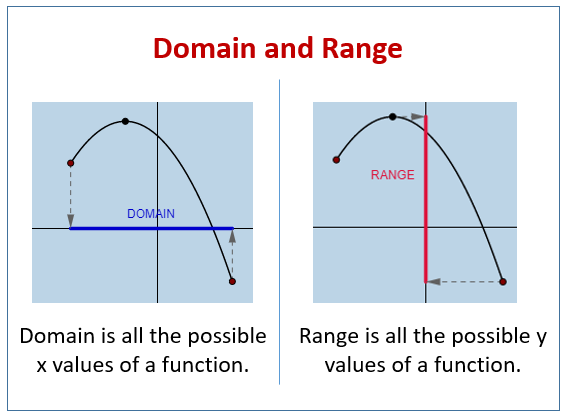
The domain is the set of numbers that can be put into a function, and the range is the set of values that come out of the function. So on a standard coordinate grid, the x values are the domain, and the y values are the range.
If you have more than one output for a particular input, then the quantities represent a relation. A graph of a relationship can be shown to be a function using the vertical line test

Create sentences
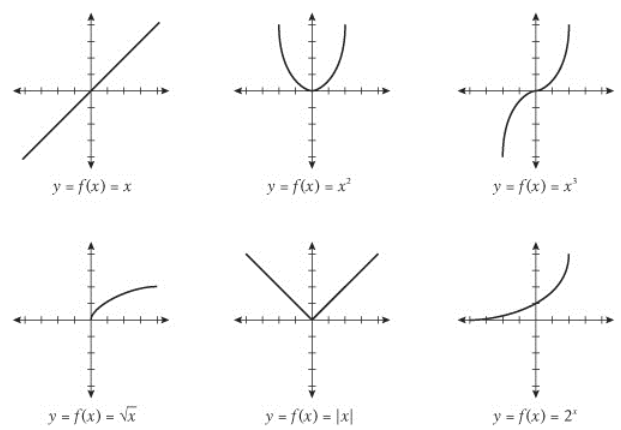
Linear Function: f(x) = mx + b.
Square Function: f(x) = x2
Square Root Function: f(x) = √x.
Absolute Value Function: f(x) = |x|
Reciprocal Function. f(x) = 1/x.
Adding and subtracting rational expressions
To add or subtract two rational expressions with the same denominator, we simply add or subtract the numerators and write the result over the common denominator. When the denominators are not the same, we must manipulate them so that they become the same.

Multiplying and dividing rational expressions
Completely factor all numerators and denominators.
Reduce all common factors.
Either multiply the denominators and numerators or leave the answer in factored form. (if dividing, multiply fractions with a reciprocal)

RESTRICTIONS
A rational expression is a ratio of two polynomials. The domain of a rational expression is all real numbers except those that make the denominator equal to zero