Chapter 10: Measurement: Length, Area, and Volume

The Metric (SI) System-System with units related by powers of 10 described by a prefix system

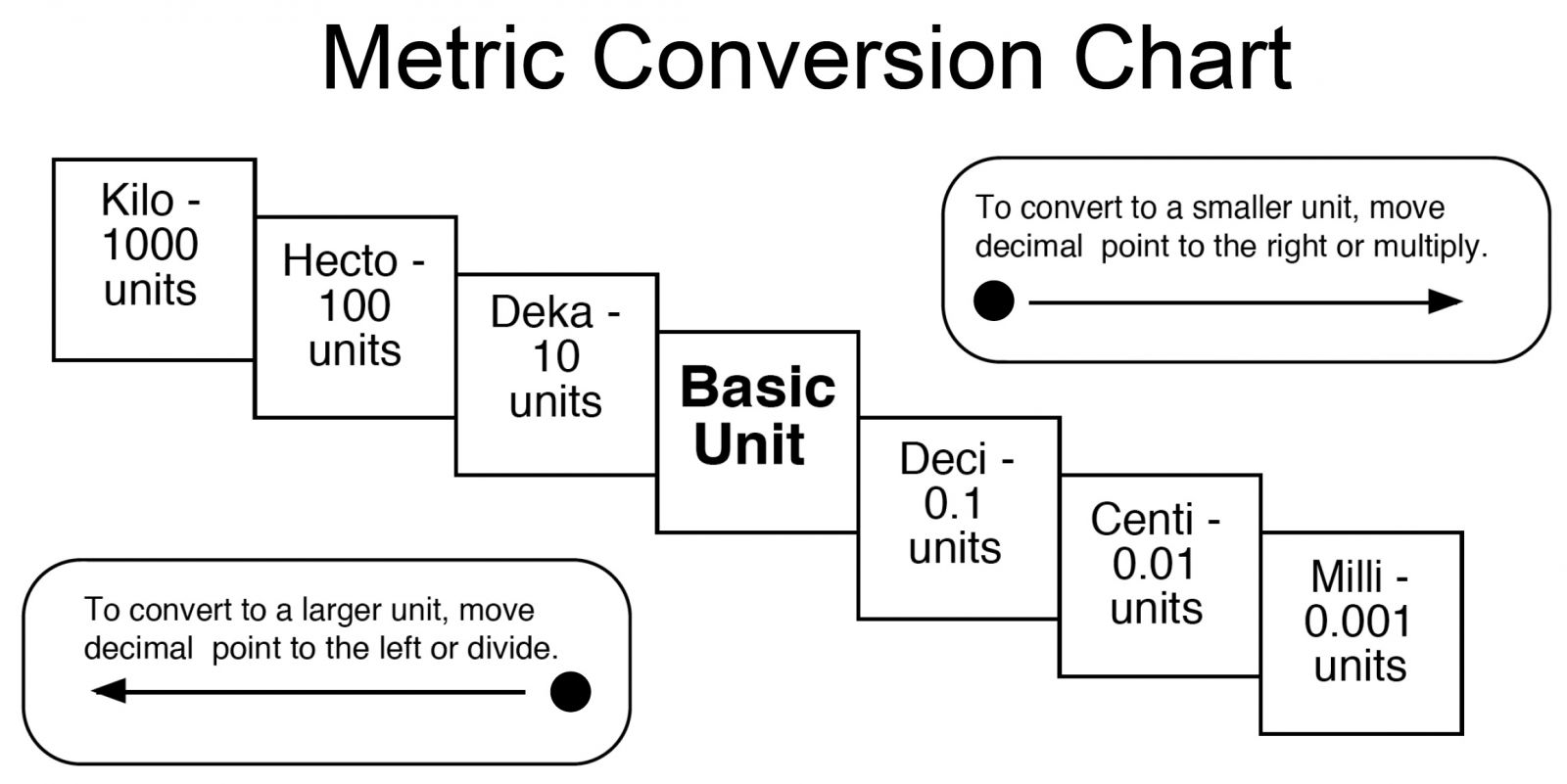
Metric units-Basic unit of length is the meter, with area given in square meters of hectares and volume in cubic meters. Capacity is also given in liters. Mass is given in Grams

Fahrenheit Temperature Scale-Scale used to measure temperature where 32 degrees is the freezing point of water and 212 degrees is the boiling point

Celsius Temperature Scale-Scale used to measure temperature with 0 degrees as the freezing point of water and 100 degrees as the boiling point

U.S. Customary System-Standardized measurement system with well-define units used to communicate size and magnitude

U.S. Customary Units-inch, foot, year, and mile for length; inches squared, feet squared, yard squared, acre, and miles squared for areal and inches cubed, feet cubed, and yards cubed, quart, and gallon for volume and capacity

Weight-The force exerted on the object by gravity

Conversions between Customary and Metric System-1 meter is about 3.28 ft and 1 ft is about .3048 meters.

Unit-Length of measurement

Standardized-To be uniform, or the same, throughout

Tanagram-Chinese geometric puzzle that is cut into 7 pieces to make various shapes

Measurement Process-A sequence of steps that is used in the measuring process

Measurable Attribute-A property of an object, such as length, area, volume, capacity, temperature, time or weight, which is to be measured

Surface Area of a Right Prism or Right Cylinder-Let a right prism or cylinder have Height (H) and bases of area (B), and let P be the perimeter of each base, 2B + B X H=SA

Surface Area of a Right Regular Pyramid-Base plus 1/2 multiplied by perimeter (P) and slant height (H), B + 1/2 X P X S=SA

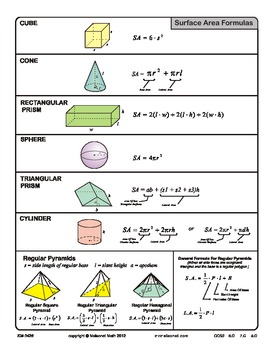
Surface Area of Right Circular Cones-Pi (3.14) multiplied by radius squared (r^2) added to Pi (3.14) multiplied by radius (R) and slant height (S), 3.14 X R^2 + 3.14 X R X S=SA

Surface Area of a Sphere-4 Multiplied by Pi (3.14) and radius squared (R^2), 4 X 3.14 X R^2=SA

The Similarity Principle of Measurement-Let Figures I and II be similar. Suppose some length dimension of Figure II of K times the corresponding dimension of Figure I; that is, K is the scale factor. Then:
(i) any length measurement--perimeter, diameter, height, slant height, and so on--of Figure II is K times that of the corresponding length measurement of Figure I
(ii) any area measurement--surface area, area of a base, lateral surface area, and so on--of Figure II is K^2 times that of the corresponding area measurement of figure I and;
(iii) any volume measurement--total volume, capacity, half-fullness, and so on of Figure II is K^3 times the corresponding volume measurement of Figure I

Volume of a Rectangular Box- Length (L)
multiplied by Width (W) multiplied by
Height (H);L X W X H=V

Volume of a Right Prism or Right Cylinder-
Base (B) multiplied by Height (H), B X H=V

Volume of General Prism or Cylinder-
Base (B) multiplied by Height (H), B X H=V

Volume of a Pyramid or Cone-
1/3 of Base (B) multiplied by Height (H),
1/3 X B X H=V

Volume of a Sphere- 4/3 of Pi (3.14)
multiplied by radius cubed (r^3)
,4/3 X 3.14 X r^3=V

Surface Area- A measurement of the
outermost layer of an object

Volume-Space that an object occupies

Area-The measurement of the inside space within an object

Perimeter-The measurement of the outside of an object. If it is closed by a curve, then the length of the curve is added

Unit of Area-Any measurement that tiles a plane. IE: in^2, ft^2

Lattice Polygons-A polygon formed by joining points of a square array

Circumference-Measurement of the outside of a circle

Congruence of Two Regions in the Plane-If R and S are regions in the plane that have the same size and shape, then they are congruent

The Congruence and Addition Properties of Area-If region R is congruent to region S, then the two regions have the same area

Addition Property-If a region R is dissected into non-overlapping sub-regions, then the sum of the sub-regions is equal to the area of the whole region

Area of a Rectangle-Length (L) multiplied by its Width (W), L X W=A

Area of a Parallelogram-Base (B) multiplied by its Height (H), B X H=A

Area of a Triangle-1/2 of the base (B) multiplied by its Height (H), B/2 X H=A

Area of a Trapezoid- 1/2 of Base 1(B1) added to Base (B2) multiplied by Height (H), 1/2(B1+B2) X H=A

Length of a Polygonal Curve-Obtained by summing the length of its sides, S+S+S=L

Length of a Non-Polygonal Curve-Measure, or estimate, the length of the approximating polygonal curve with vertices on the given curve

Circumference of a Circle-Diameter (D) of a circle multiplied by Pi (3.14), D X 3.14=C

Area of a Circle-Pi (3.14) multiplied by radius (R) squared, 3.14 X R^2=A

The Pythagorean Theorem-Used to find missing side lengths within a right triangle

Converse of the Pythagorean Theorem-Let a triangle have side of length a, b, and c. If a^2+b^2=c^2, then the triangle is a right triangle and the angle opposite of the side of length c is a right angle

The Pythagorean Theorem-Leg 1 squared (A^2) multiplied by Leg 2 squared (B^2)equals Hypotenuse squared (C^2)