Conicas
Cicunferencia
Definición
Curva plana y cerada
Todos los puntos a = distancia del centro

Grafico:
Elementos:
Centro
Circunferencia
Radio
Diámetro
Ecuaciones:
Para cualquier punto P(x,y)
Cuyo centro es C(a,b)
Y con radio -
la ecuación es
(x-a)^2+(y-b)^2=r^2
Ejemplo
Tenemos una circunferencia con r=6,5 P(7,-3) Pc(2,1) P(-3,5)
(-3-2)^2+(5-1)^2=r^2
r=6,5
Parabola
Definición
Curva abierta formada por
dos ramas simetricas respecto a un eje
y en que todos sus puntos están a la misma distancia del foco y la directriz
Elementos
foco
Directriz
parametro
eje
vertice
Radio vector
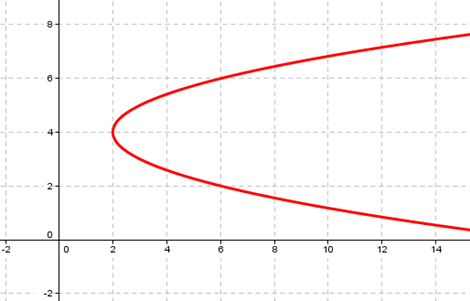
Grafico
Ecuaciones

ax^2+bx+c=0
Ejemplo
y = -x² + 4x - 3
x² − 4x + 3 = 0


Elipse:
Definición
Curva cerrada
dos ejes de simetria
sale de cortar la superficie de un cono por un pano oblicuo al eje de simetría
Elementos:
focos
eje focal
eje secundario
centro
radios vectores
distancia focal
vértices
Eje mayor
eje menor
ejes de simetría
centro de simetría

Grafico
Ecuaciones:
Eje mayor es horizontal
(x−x0)^2/a^2+(y−y0)^2/b^2=1
Eje mayor es vertical
(x−x0)^2/b^2+(y−y0)^2/a^2=1
e=√1−b^2/a^2
Ejemplo
x2/16+y^2/4=1
e=√1−b^2/a^2
e=√1−4/16
e=√3/4
Hipérbola:
Definición
Es una curva abierta de dos ramas obtenida
cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría
con ángulo menor que el de la generatriz respecto del eje de revolución.
Elementos
Focos
Centro
Vertices
Eje focal

Gráfico
Ecuaciones
(x^2/a^2)-(y^2/b^2)=1
Asintotas
y=+-b/a x
Ejemplo
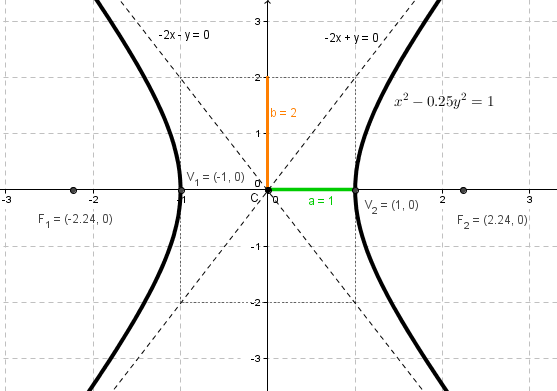
x^2-(y^2/4)=1
C(0,0)
Semieje real: a=1
Semidistancia focal :c=√1^2+2^2=√5
V1(1,0) V2(-1,0) F1(-√
5,0) F2(√
5,0)
Asíntotas: y=+-2x